题目内容
【题目】已知点![]() 为抛物线
为抛物线![]() :
: ![]() 的焦点,点
的焦点,点![]() 为抛物线
为抛物线![]() 上一定点。
上一定点。
(1)直线![]() 过点
过点![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过点![]() 作两条倾斜角互补的直线分别交抛物线
作两条倾斜角互补的直线分别交抛物线![]() 于异于点
于异于点![]() 的两点
的两点![]() ,试证明直线
,试证明直线![]() 的斜率为定值,并求出该定值。
的斜率为定值,并求出该定值。
【答案】(Ⅰ)![]() ,或
,或![]() ;(Ⅱ)1.
;(Ⅱ)1.
【解析】试题分析:(1)依题意,点![]() 的坐标为
的坐标为![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,
,
联立方程组: ![]() ,消去
,消去![]() 并整理得:
并整理得: ![]() ,设
,设![]() ,则
,则![]() 故
故![]() 解得
解得![]() ,写出直线
,写出直线![]() 的方程(2)过点
的方程(2)过点![]() 作两条倾斜角互补的直线分别交抛物线
作两条倾斜角互补的直线分别交抛物线![]() 于异于点
于异于点![]() 的两点
的两点![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .令
.令![]() ,联立方程组:
,联立方程组: ![]() ,消去
,消去![]() 并整理得:
并整理得: ![]() 设
设![]() ,因为点
,因为点![]() 的坐标为
的坐标为![]() ,所以
,所以![]() ,故
,故![]() ,用-t去换点P坐标中的t可得点
,用-t去换点P坐标中的t可得点![]() 的坐标为
的坐标为![]() ,计算直线
,计算直线![]() 的斜率即可.
的斜率即可.
试题解析:
(1)依题意,点![]() 的坐标为
的坐标为![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,
,
联立方程组: ![]() ,消去
,消去![]() 并整理得:
并整理得: ![]()
设![]() ,则
,则![]()
故![]() ,解得:
,解得: ![]() .
.
故直线![]() 的方程为
的方程为![]() ,或
,或![]() .
.
(2)设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .令
.令![]() ,
,
联立方程组: ![]() ,消去
,消去![]() 并整理得:
并整理得: ![]()
设![]() ,因为点
,因为点![]() 的坐标为
的坐标为![]() ,所以
,所以![]() ,故
,故![]() ,
,
从而点![]() 的坐标为
的坐标为![]() ,用-t去换点P坐标中的t可得点
,用-t去换点P坐标中的t可得点![]() 的坐标为
的坐标为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为 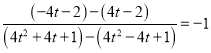

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目