题目内容
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900.
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
(1)见试题解析;(2) .
.
解析试题分析:(1)要证两直线垂直,一般通过证明其中一条直线垂直于过另一条直线的平面,这里观察已知,有PD⊥平面ABCD,则有PD⊥BC,又BC⊥CD,显然就有BC⊥平面PCD,问题得证;(2)要求点A到平面PBC的距离,由于三棱锥P-ABC的体积容易求出(底面是三角形ABC,高是PD),故可用体积法求点A到平面PBC的距离,见解法二.当然题中由于 且
且 ,故A到平面PBC的距离等于D到平面PBC的距离的2倍,从而可能先求点D到平面PBC的距离,此时直接作出垂线段即可,见解法一.
,故A到平面PBC的距离等于D到平面PBC的距离的2倍,从而可能先求点D到平面PBC的距离,此时直接作出垂线段即可,见解法一.
试题解析:(1)证明:因为PD⊥平面ABCD,BC 平面ABCD,所以PD⊥BC.
平面ABCD,所以PD⊥BC.
由∠BCD=900,得CD⊥BC,
又PD DC=D,PD、DC
DC=D,PD、DC 平面PCD,
平面PCD,
所以BC⊥平面PCD.
因为PC 平面PCD,故PC⊥BC.
平面PCD,故PC⊥BC.
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等.又点A到平面PBC的距离等于E到平面PBC的距离的2倍.由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F.易知DF= ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于 .
.
(方法二)体积法:连结AC.设点A到平面PBC的距离为h.
因为AB∥DC,∠BCD=900,所以∠ABC=900.
从而AB=2,BC=1,得 的面积
的面积 .
.
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积 .
.
因为PD⊥平面ABCD,DC 平面ABCD,所以PD⊥DC.
平面ABCD,所以PD⊥DC.
又PD=DC=1,所以 .
.
由PC⊥BC,BC=1,得 的面积
的面积 .
.
由 ,
, ,得
,得 ,
,
故点A到平面PBC的距离等于 .
.
考点:(1)线面垂直与线线垂直;(2)点到平面的距离.

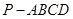 中,
中,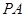 ⊥面
⊥面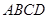 ,
,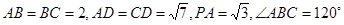
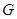 为线段
为线段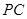 上的点.
上的点.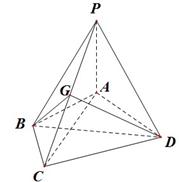
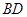 ⊥面
⊥面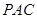 ;
; 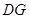 与
与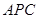 所成的角的正切值;
所成的角的正切值;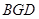 ,求
,求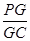 的值.
的值.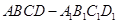 中,
中,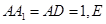 为线段
为线段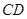 中点.
中点.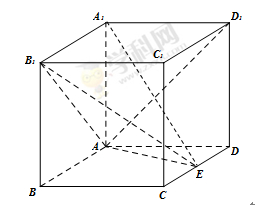
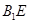 与直线
与直线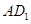 所成的角的余弦值;
所成的角的余弦值;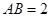 ,求二面角
,求二面角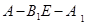 的大小;
的大小;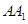 上是否存在一点
上是否存在一点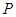 ,使得
,使得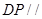 平面
平面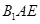 ?若存在,求
?若存在,求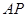 的长;若不存在,说明理由.
的长;若不存在,说明理由. 中,底面△
中,底面△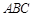 为等腰直角三角形,
为等腰直角三角形,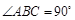 ,
, 为棱
为棱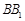 上一点,且平面
上一点,且平面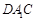 ⊥平面
⊥平面 .
.
 为何值时,二面角
为何值时,二面角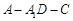 的平面角为
的平面角为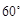 .
.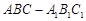 中,
中,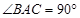 ,
,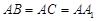 ,且
,且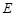 是
是 中点.
中点.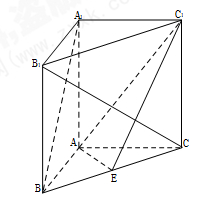
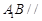 平面
平面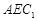 ;
;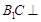 平面
平面 .
. 中,侧面
中,侧面 与底面
与底面 垂直,
垂直,  分别是
分别是 的中点,
的中点,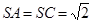 ,
,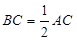 ,
,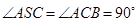 .
.
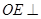 平面
平面 ;
;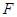 为线段
为线段 的中点,求异面直线
的中点,求异面直线 与
与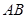 所成角的正切值.
所成角的正切值. 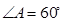 、边长为
、边长为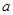 的菱形,又
的菱形,又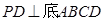 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.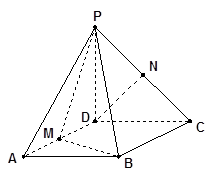
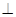 平面PAD;
平面PAD;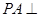 平面
平面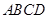 ,四边形
,四边形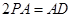 ,
,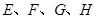 分别是线段
分别是线段 的中点.
的中点.
 平面
平面 ;
;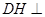 平面
平面 ;
;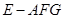 与四棱锥
与四棱锥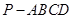 的体积比.
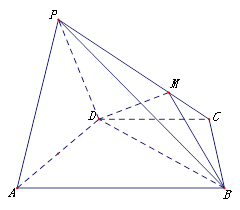
的体积比.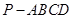 中,平面
中,平面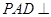 平面
平面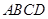 ,
,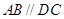 ,
,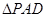 是等边三角形,已知
是等边三角形,已知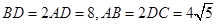 .
.
 是
是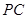 上的一点,证明:平面
上的一点,证明:平面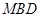 ;
;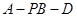 的余弦值.
的余弦值.