题目内容
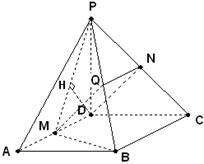
已知四棱锥P-ABCD,底面ABCD是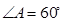 、边长为
、边长为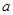 的菱形,又
的菱形,又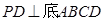 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.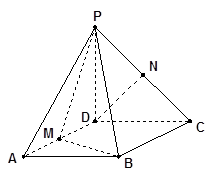
(1)证明:MB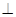 平面PAD;
平面PAD;
(2)求点A到平面PMB的距离.
(1)证明见解析;(2)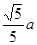 .
.
解析试题分析:(1)易证 ,又因为底面
,又因为底面 是
是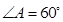 ,边长为
,边长为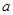 的菱形,且
的菱形,且 为
为 中点,得
中点,得 ,最后由线面垂直的判定定理即可证明
,最后由线面垂直的判定定理即可证明 面
面 ;
;
(2)因为 是
是 中点,所以点
中点,所以点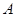 与
与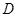 到平面
到平面 等距离,过点
等距离,过点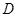 作
作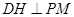 于
于 ,由(1)可得平面
,由(1)可得平面 平面
平面 ,所以
,所以 平面
平面 ,
, 是点
是点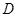 到平面
到平面 的距离,从而求解.
的距离,从而求解.
试题解析:(1)因为 平面
平面 ,
, 平面
平面
所以
又因为底面 是
是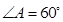 、边长为
、边长为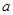 的菱形,且M为AD中点,
的菱形,且M为AD中点,
所以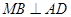 .
.
又
所以 平面
平面
(2)因为 是
是 中点,所以点
中点,所以点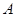 与
与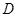 到平面
到平面 等距离
等距离
过点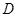 作
作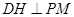 于
于 ,
,
由(1)得 平面
平面 ,又
,又 面
面 ,所以平面
,所以平面 平面
平面 ,
,
所以 平面
平面 .
.
故 是点
是点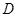 到平面
到平面 的距离
的距离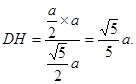
所以点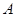 到平面
到平面 的距离为
的距离为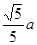 .
.
考点:1.直线与平面垂直的判定和性质;2.点、线、面间的距离计算.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 中,已知平面
中,已知平面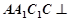 平面
平面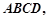 且
且 ,
, .
.

 为棱
为棱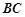 的中点,求证:
的中点,求证: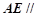 平面
平面 .
. 中,
中,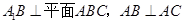 .
.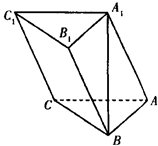
 ;
; ,在棱
,在棱 上确定一点P, 使二面角
上确定一点P, 使二面角 的平面角的余弦值为
的平面角的余弦值为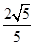 .
.
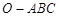 的侧棱
的侧棱 两两垂直,且
两两垂直,且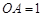 ,
,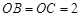 ,
,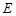 是
是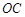 的中点。
的中点。
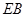 与
与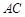 所成角的余弦值;
所成角的余弦值;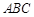 的所成角的正弦值。
的所成角的正弦值。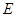 是以
是以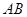 为直径的半圆上异于点
为直径的半圆上异于点 的点,矩形
的点,矩形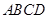 所在的平面垂直于该半圆所在平面,且
所在的平面垂直于该半圆所在平面,且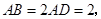
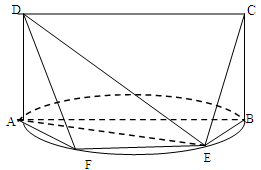
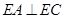 ;
;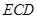 与半圆弧的另一个交点为
与半圆弧的另一个交点为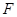 ,
,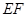 //
//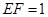 ,求三棱锥E-ADF的体积.
,求三棱锥E-ADF的体积. 中,
中, 是边长为2的正三角形,平面
是边长为2的正三角形,平面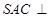 平面
平面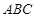 ,
,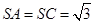 ,
,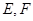 分别为
分别为 的中点.
的中点.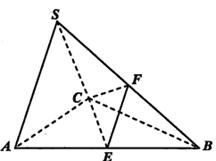
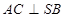 ;
; 的余弦值;
的余弦值;
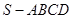 的底面是正方形,
的底面是正方形, 底面
底面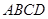 ,
,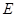 是
是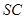 上一点
上一点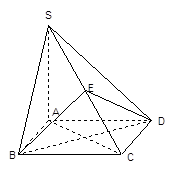
 平面
平面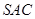 ;
;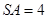 ,
, ,求点
,求点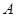 到平面
到平面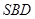 的距离.
的距离.