题目内容
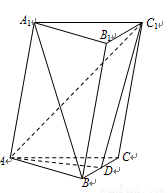
(本题满分14分)如图,已知斜三棱柱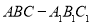 中,
中,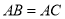 ,
,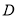 为
为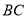 的中点.
的中点.
(1)若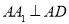 ,求证:
,求证: ;
;
(2)求证: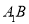 // 平面
// 平面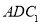
(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)由等腰三角形底边中线即为高线可得 .由
.由 ,
, 可得
可得 ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得 平面
平面 ,从而可得
,从而可得 .(2) 连结
.(2) 连结 交
交 于点
于点 ,连结
,连结 , 则
, 则 为
为 的中点.由中位线可得
的中点.由中位线可得 .根据线面平行的判定定理可证得
.根据线面平行的判定定理可证得 平面
平面 .
.
试题解析:证明:

(1)因为 ,
, 为
为 的中点,所以
的中点,所以 . 2分
. 2分
因为 ,
, ,所以
,所以 , 4分
, 4分
 ,所以
,所以 平面
平面 , 6分
, 6分
因为 平面
平面 所以
所以 7分
7分
(2)连结 交
交 于点
于点 ,连结
,连结 , 则
, 则 为
为 的中点.
的中点.
因为 为
为 的中点,所以
的中点,所以 9分
9分
因为 平面
平面 ,
,  平面
平面 , 12分
, 12分
所以 平面
平面 14分
14分
考点:1线线垂直,线面垂直;2线面平行.

练习册系列答案
相关题目
两圆 与
与 的公切线有( )条
的公切线有( )条
A. | B. | C. | D. |
抛物线y2=2px,(p>0)绕焦点依逆时针方向旋转90°所得抛物线方程为( )
| A.x2=2py |
B. |
C. |
D. |
 与圆
与圆 相外切, 则
相外切, 则 的最大值为 ( )
的最大值为 ( ) B.
B. C.
C. D.
D.
 ,则“
,则“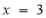 ”是“
”是“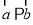 ”的( )
”的( ) 与双曲线
与双曲线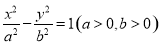 有相同的焦点
有相同的焦点 ,点
,点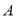 是两曲线的一个交点,且
是两曲线的一个交点,且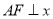 轴,则双曲线的离心率为 .
轴,则双曲线的离心率为 .  且与直线
且与直线 垂直的直线的方程为 ;
垂直的直线的方程为 ;  ,(
,(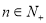 ),则在数列{
),则在数列{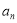 }的前50项中最小项和最大项分别是( )
}的前50项中最小项和最大项分别是( )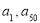 B.
B.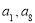 C.
C.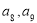 D.
D.
 ,则
,则 的大小关系是( )
的大小关系是( ) B.
B.  C.
C.  D.
D. 