题目内容
如图,已知正方形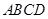 的边长为
的边长为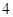 ,
,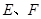 分别是
分别是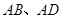 的中点,
的中点,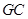 ⊥平面
⊥平面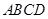 ,且
,且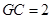 ,则点
,则点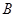 到平面
到平面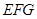 的距离为
的距离为
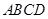 的边长为
的边长为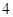 ,
,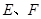 分别是
分别是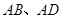 的中点,
的中点,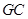 ⊥平面
⊥平面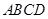 ,且
,且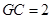 ,则点
,则点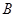 到平面
到平面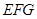 的距离为
的距离为 
A.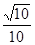 | B.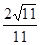 | C.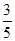 | D.1 |
B
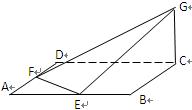
试题分析:以C为原点CD为x轴CB为y轴CG为z轴建立空间坐标系,

 所以平面
所以平面 的一个法向量为
的一个法向量为

点评:空间向量求解立体几何题目关键是建立合适的坐标系找到相关点的坐标

练习册系列答案
相关题目
题目内容
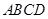 的边长为
的边长为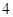 ,
,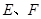 分别是
分别是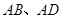 的中点,
的中点,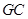 ⊥平面
⊥平面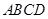 ,且
,且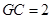 ,则点
,则点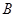 到平面
到平面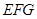 的距离为
的距离为 
A.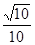 | B.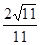 | C.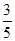 | D.1 |

 所以平面
所以平面 的一个法向量为
的一个法向量为

