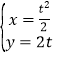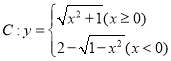Question

【题目】已知抛物线C的顶点在原点，对称轴是y轴，直线与抛物线交于不同的两点、，线段中点的纵坐标为2，且.

（1）求抛物线的标准方程；

（2）设抛物线的焦点为，若直线经过焦点，求直线的方程.

Answer 1

【答案】（1）；

（2）；

【解析】

（1）根据题中所给的条件，判断出抛物线的焦点所在轴以及开口方向，从而设出抛物线的标准方程为，根据定义列出等量关系式，求得，得到抛物线的方程；

（2）根据题意，设出直线的方程为，与抛物线的方程联立消元得到，利用题意，列出等量关系式，求得k=±，得到结果.

（1）由题意可设抛物线C的标准方程为：，

设，则

∵，∴，所以抛物线C的方程为：

（2）由已知得k一定存在且;故可设直线的方程为：，

则联立直线与抛物线方程，整理可得：

由韦达定理得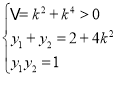，∴=4解得：k=±，

故所求直线方程为.