题目内容
设 、
、 为两非零向量,且满足|
为两非零向量,且满足| |+|
|+| |=2,2
|=2,2 •
• =
= 2•
2• 2,则两向量
2,则两向量 、
、 的夹角的最小值为 .
的夹角的最小值为 .
【答案】分析:设两向量 、
、 的夹角为θ,|
的夹角为θ,| |=t(t>0),由已知可得,2|
|=t(t>0),由已知可得,2| ||
|| |cosθ=
|cosθ= ,即cosθ=
,即cosθ= =
= (t>0),根据二次函数的性质可求cosθ的最小值,即可求解θ的最大值
(t>0),根据二次函数的性质可求cosθ的最小值,即可求解θ的最大值
解答:解:设两向量 、
、 的夹角为θ,|
的夹角为θ,| |=t(t>0)
|=t(t>0)
∵| |+|
|+| |=2,则|
|=2,则| |=2-t
|=2-t
∵2 •
• =
= 2•
2• 2,
2,
∴2| ||
|| |cosθ=
|cosθ=
∴cosθ= =
= (t>0)
(t>0)
设f(t)= (t>0),根据二次函数的性质可知,当t=1,f(t)有最大值
(t>0),根据二次函数的性质可知,当t=1,f(t)有最大值
∴cosθ
∴ 即最小值为
即最小值为
故答案为:
点评:本题主要考查了向量的数量积的定义、性质的应用,二次函数的性质的应用,属于知识的综合应用
 、
、 的夹角为θ,|
的夹角为θ,| |=t(t>0),由已知可得,2|
|=t(t>0),由已知可得,2| ||
|| |cosθ=
|cosθ= ,即cosθ=
,即cosθ= =
= (t>0),根据二次函数的性质可求cosθ的最小值,即可求解θ的最大值
(t>0),根据二次函数的性质可求cosθ的最小值,即可求解θ的最大值解答:解:设两向量
 、
、 的夹角为θ,|
的夹角为θ,| |=t(t>0)
|=t(t>0)∵|
 |+|
|+| |=2,则|
|=2,则| |=2-t
|=2-t∵2
 •
• =
= 2•
2• 2,
2,∴2|
 ||
|| |cosθ=
|cosθ=
∴cosθ=
 =
= (t>0)
(t>0)设f(t)=
 (t>0),根据二次函数的性质可知,当t=1,f(t)有最大值
(t>0),根据二次函数的性质可知,当t=1,f(t)有最大值
∴cosθ

∴
 即最小值为
即最小值为
故答案为:

点评:本题主要考查了向量的数量积的定义、性质的应用,二次函数的性质的应用,属于知识的综合应用

练习册系列答案
相关题目
 、
、 为两非零向量,且满足
为两非零向量,且满足 ,则两向量
,则两向量 、
、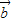 为两非零向量,且满足
为两非零向量,且满足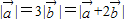 ,则两向量
,则两向量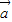 、
、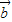 的夹角的余弦值为 .
的夹角的余弦值为 .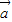 、
、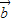 为两非零向量,且满足|
为两非零向量,且满足|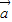 |=2|
|=2|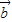 |=|2
|=|2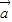 +3
+3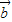 |,则两向量
|,则两向量 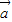 、
、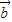 的夹角的余弦值为 .
的夹角的余弦值为 .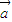 、
、 为两非零向量,且满足|
为两非零向量,且满足|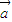 |+|
|+|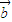 |=2,2
|=2,2 •
•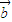 =
= 2•
2•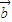 2,则两向量
2,则两向量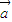 、
、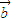 的夹角的最小值为 .
的夹角的最小值为 .