题目内容
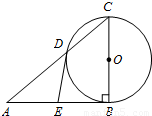
 如图,直角△ABC中,∠A=30°,∠B为直角,BC=1,D,E分别是AC,AB上的动点,且
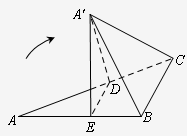
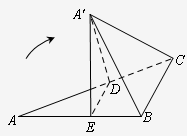
如图,直角△ABC中,∠A=30°,∠B为直角,BC=1,D,E分别是AC,AB上的动点,且DE∥BC,现将△ADE沿DE翻折,使得平面A'DE⊥平面BCDE,当DE运动时,四棱锥A'-BCDE体积的最大值为
分析:由题意设出AE=x,求出ED,然后求出四棱锥A'-BCDE体积的表达式,利用函数的导数求出函数的最大值即可.
解答: 解:设AE=x,x∈(0,
解:设AE=x,x∈(0,
),所以ED=
,所以四棱锥A'-BCDE体积:V=
x(
-
×
x2)=
x-
x3,
所以V′=
-
x2,令V′=0,解得x=1,x∈(0,1)函数单调递增,x∈[1,
)导数小于0,函数单调递减,所以x=1时,四棱锥A'-BCDE体积取得最大值,就是
-
=
;
故答案为:
.
 解:设AE=x,x∈(0,
解:设AE=x,x∈(0,| 3 |
| ||
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
| ||
| 18 |
所以V′=
| ||
| 6 |
| ||
| 6 |
| 3 |
| ||
| 6 |
| ||
| 18 |
| ||
| 9 |
故答案为:
| ||
| 9 |
点评:本题是中档题,考查棱锥的体积的求法,利用导数求解函数的最大值的方法,考查计算能力,空间想象能力.

练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲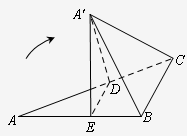 如图,直角△ABC中,∠A=30°,∠B为直角,BC=1,D,E分别是AC,AB上的动点,且
如图,直角△ABC中,∠A=30°,∠B为直角,BC=1,D,E分别是AC,AB上的动点,且 ,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.
,点P(2,-1)在矩阵A对应的变换下得到点P′(5,1),求矩阵A.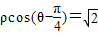 ,曲线C的参数方程为
,曲线C的参数方程为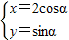 (α为参数),求曲线C截直线l所得的弦长.
(α为参数),求曲线C截直线l所得的弦长.