题目内容
如图1-1，在△ABC中，a、b、c分别为角A、B、C的对边，a2+b2-c2=ab，CM是△ABC外接圆的直径，BM=11，AM=2，求CM的长．
思路分析：要求出三角形外接圆直径长，根据正弦定理，只要求出△ABC的一个内角和它的对边．由题设等式的特点，利用余弦定理可求∠ACB，接着它的对边AB在△ABC中可求，问题得到解决．
解：由余弦定理
cos∠ACB=
=
=
，
∴∠ACB=60°.
于是∠AMB=120°.
在△ABM中，由余弦定理
AB2=BM2+AM2-2BM\5AMcos120°
=121+4-2×11×2×(-
)
=147，
即AB=73.
∴CM=
=
=14.
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
如图所示，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4．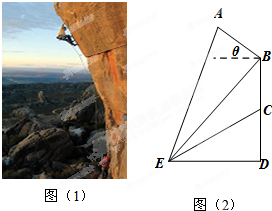
攀岩运动是一项刺激而危险的运动，如图（1）在某次攀岩活动中，两名运动员在如图所在位置，为确保运动员的安全，地面救援者应时刻注意两人离地面的距离，以备发生危险时进行及时救援．为了方便测量和计算，画出示意图，如图（2）所示，点A，C分别为两名攀岩者所在位置，点B为山的拐角处，且斜坡AB的坡角为θ，点D为山脚，某人在地面上的点E处测得A，B，C的仰角分别为α，β，γ，ED=a，求：
AD，若EG=5 cm，则AC=______________；若BD=20 cm，则EF=______________.
，设这条最短路线与CC1的交点为N.求： 