题目内容
已知点P为椭圆 上一点,A、B为椭圆
上一点,A、B为椭圆 =1上不同的两点,且
=1上不同的两点,且 ,若OA、OB所在的直线的斜率为k1、k2,则k1•k2= .
,若OA、OB所在的直线的斜率为k1、k2,则k1•k2= .
【答案】分析:设A(x1,y1),B(x2,y2),P(x,y).利用点与椭圆的关系可得 ,
, ,
, .再利用向量的运算
.再利用向量的运算 ,可得
,可得 ,代入点P满足的椭圆方程即可得出.
,代入点P满足的椭圆方程即可得出.
解答:解:设A(x1,y1),B(x2,y2),P(x,y).
则 ,
, ,
, .
.
∵ ,∴
,∴ ,代入上述方程得
,代入上述方程得
 ,
,
∴ +
+ ,
,
∴ ,
,
得 =-
=- .
.
故答案为- .
.
点评:熟练掌握点与椭圆的关系、向量的运算与相等、斜率的计算公式等是解题的关键.
 ,
, ,
, .再利用向量的运算
.再利用向量的运算 ,可得
,可得 ,代入点P满足的椭圆方程即可得出.
,代入点P满足的椭圆方程即可得出.解答:解:设A(x1,y1),B(x2,y2),P(x,y).
则
 ,
, ,
, .
.∵
 ,∴
,∴ ,代入上述方程得
,代入上述方程得 ,
,∴
 +
+ ,
,∴
 ,
,得
 =-
=- .
.故答案为-
 .
.点评:熟练掌握点与椭圆的关系、向量的运算与相等、斜率的计算公式等是解题的关键.

练习册系列答案
相关题目
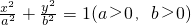 上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若
上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若 且△PF1F2的面积为
且△PF1F2的面积为 (c为椭圆半焦距)则椭圆的离心率为________.
(c为椭圆半焦距)则椭圆的离心率为________. 上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若
上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若 且△PF1F2的面积为
且△PF1F2的面积为 (c为椭圆半焦距)则椭圆的离心率为 .
(c为椭圆半焦距)则椭圆的离心率为 . 上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若
上一点,F1,F2为椭圆的左、右焦点.O为坐标原点,若 且△PF1F2的面积为
且△PF1F2的面积为 (c为椭圆半焦距)则椭圆的离心率为 .
(c为椭圆半焦距)则椭圆的离心率为 .