题目内容
已知点P为椭圆
上一点，F1，F2为椭圆的左、右焦点．O为坐标原点，若
且△PF1F2的面积为
（c为椭圆半焦距）则椭圆的离心率为 ．
【答案】分析：先确定△PF1F2为直角三角形，再结合椭圆的定义，三角形的面积，建立方程，即可求得结论．
解答：解：由题意，∵若
，∴△PF1F2为直角三角形
设|PF1|=m，|PF2|=n，则m+n=2a，
mn=
，m2+n2=4c2，
∴4a2-2
ac=4c2，
∴e2+
e-1=0
∵0＜e＜1，∴e=
故答案为：
点评：本题考查椭圆的离心率，考查椭圆的定义，考查学生的计算能力，属于基础题．
解答：解：由题意，∵若
，∴△PF1F2为直角三角形设|PF1|=m，|PF2|=n，则m+n=2a，
mn=，m2+n2=4c2，∴4a2-2
ac=4c2，∴e2+
e-1=0∵0＜e＜1，∴e=
故答案为：
点评：本题考查椭圆的离心率，考查椭圆的定义，考查学生的计算能力，属于基础题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
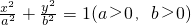上一点，F1，F2为椭圆的左、右焦点．O为坐标原点，若
且△PF1F2的面积为
（c为椭圆半焦距）则椭圆的离心率为________．
上一点，F1，F2为椭圆的左、右焦点．O为坐标原点，若
且△PF1F2的面积为
（c为椭圆半焦距）则椭圆的离心率为 ．
上一点，A、B为椭圆
=1上不同的两点，且
，若OA、OB所在的直线的斜率为k1、k2，则k1•k2= ．