题目内容
已知函数![]() 在
在![]() 处取到极值2
处取到极值2
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设函数![]() .若对任意的
.若对任意的![]() ,总存在唯一的
,总存在唯一的![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解: (Ⅰ)![]() (2分)
(2分)
由![]() 在
在![]() 处取到极值2,故
处取到极值2,故![]() ,
,![]() 即
即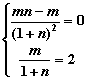 ,
,![]()
解得![]() ,经检验,此时
,经检验,此时![]() 在
在![]() 处取得极值.故
处取得极值.故![]() (4分)
(4分)
(Ⅱ)由(Ⅰ)知![]() ,故
,故![]() 在
在![]() 上单调递增,在
上单调递增,在![]()
![]() 上单调递减,由
上单调递减,由![]() ,故
,故![]() 的值域为
的值域为![]() (6分)
(6分)
依题意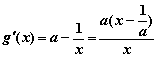 ,记
,记![]()
![]()
![]()
![]()
(ⅰ)当![]() 时,
时,![]()
![]()
![]() ,
,![]() 在
在![]() 上单调递减,依题意由
上单调递减,依题意由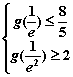 得
得![]() ,
,
故此时![]() (8分)
(8分)
(ⅱ)当![]() 时,
时,![]() >
>![]() >
>![]() 当
当![]() 时,
时,![]() <
<![]() ,当
,当![]() 时,
时,![]() >
>![]() 。依题意由
。依题意由![]() ,得
,得![]() ,即
,即![]() .与
.与![]() 矛盾 (10分)
矛盾 (10分)
(ⅲ)当![]() >
>![]() 时,
时,![]() <
<![]() ,此时
,此时![]() >
>![]() ,
,![]() 在
在![]() 上单调递增,依题意得
上单调递增,依题意得
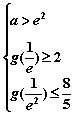 即
即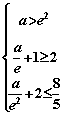 此不等式组无解(11分).综上,所求
此不等式组无解(11分).综上,所求![]() 取值范围为
取值范围为![]() (12分)
(12分)

练习册系列答案
相关题目
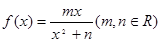 在
在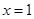 处取到极值
处取到极值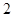
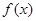 的解析式;
的解析式;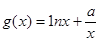 ,若对任意的
,若对任意的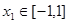 ,总存在
,总存在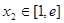 ,使得
,使得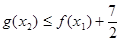 ,求实数
,求实数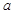 的取值范围.
的取值范围.
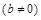 在
在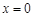 处取到极值2.
处取到极值2.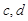 的值;
的值;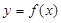 的所有切线与直线
的所有切线与直线 垂直的条数;
垂直的条数;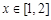 ,均存在
,均存在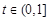 ,使得
,使得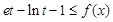 ,试求
,试求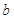 的取值范围.
的取值范围. 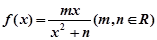 在
在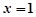 处取到极值2
处取到极值2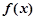 的解析式;
的解析式;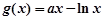 .若对任意的
.若对任意的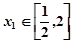 ,总存在唯一的
,总存在唯一的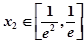 ,使得
,使得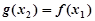 ,求实数
,求实数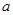 的取值范围.
的取值范围.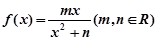 在
在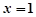 处取到极值2
处取到极值2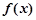 的解析式;
的解析式;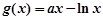 .若对任意的
.若对任意的 ,总存在唯一的
,总存在唯一的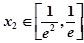 ,使得
,使得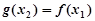 ,求实数
,求实数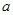 的取值范围.
的取值范围.