题目内容
一只蚂蚁在边长分别为6,8,10的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为
1-
| π |
| 48 |
1-
.| π |
| 48 |
分析:求出三角形的面积;再求出据三角形的三顶点距离小于等于1的区域为三个扇形,三个扇形的和是半圆,求出半圆的面积;利用对理事件的概率公式及几何概型概率公式求出恰在离三个顶点距离都大于1的地方的概率.
解答:解:三角形ABC的面积为 S1=
×6×8=24,
所以离三个顶点距离不都大于1的地方的面积为 S2=
π,
所以其恰在离三个顶点距离都大于1的地方的概率为:P=1-
=1-
.

故答案为:1-
.
| 1 |
| 2 |
所以离三个顶点距离不都大于1的地方的面积为 S2=
| 1 |
| 2 |
所以其恰在离三个顶点距离都大于1的地方的概率为:P=1-
| S2 |
| S1 |
| π |
| 48 |

故答案为:1-
| π |
| 48 |
点评:本题考查几何概型概率公式、对立事件概率公式、三角形的面积公式、扇形的面积公式.

练习册系列答案
相关题目
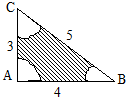 如图,一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )
如图,一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )A、
| ||
B、1-
| ||
C、1-
| ||
D、1-
|

 B.
B. C.
C. D.
D.