题目内容
设函数
，
，其中
，a、b为常数，已知曲线
与
在点（2,0）处有相同的切线l。
（I） 求a、b的值，并写出切线l的方程；
（II）若方程
有三个互不相同的实根0、
、
，其中
，且对任意的
，
恒成立，求实数m的取值范围。
（2）由（1）得
，所以
依题意，方程
有三个互不相同的实根0、x1、x2，
故x1、x2是
方程
的两相异的实根.
所以△=9-4（2-m）>0，即
又对任意的
成立.
特别地，取
时，
成立，得m<0.
由韦达定理，可得
故
对任
意的
，有
，
，x>0.
则
又
所以函数
在的最大值为0.
于是当m<0时，对任意的，
恒成立.
综上，m的取值范围是（
）.
练习册系列答案
相关题目
，
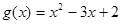，其中
，a、b为常数，已知曲线
在点（2,0）处有相同的切线
。
单调区间与极值。
，
，其中
，a、b为常数，已知曲线
与
在点（2,0）处有相同的切线l。
有三个互不相同的实根0、
、
，其中
，且对任意的
，
恒成立，求实数m的取值范围。