题目内容
(2012•湖北)已知向量
=(cosωx-sinωx,sinωx),
=(-cosωx-sinωx,2
cosωx),设函数f(x)=
•
+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈(
,1)
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
,0)求函数f(x)在区间[0,
]上的取值范围.
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
| π |
| 4 |
| 3π |
| 5 |
分析:(1)先利用向量数量积运算性质,求函数f(x)的解析式,再利用二倍角公式和两角差的余弦公式将函数f(x)化为y=Asin(ωx+φ)+k型函数,最后利用函数的对称性和ω的范围,计算ω的值,从而得函数的最小正周期;
(2)先将已知点的坐标代入函数解析式,求得λ的值,再求内层函数的值域,最后将内层函数看做整体,利用正弦函数的图象和性质即可求得函数f(x)的值域.
(2)先将已知点的坐标代入函数解析式,求得λ的值,再求内层函数的值域,最后将内层函数看做整体,利用正弦函数的图象和性质即可求得函数f(x)的值域.
解答:解:(1)∵f(x)=
•
+λ=(cosωx-sinωx)×(-cosωx-sinωx)+sinωx×2
cosωx+λ
=-(cos2ωx-sin2ωx)+
sin2ωx+λ
=
sin2ωx-cos2ωx+λ=2sin(2ωx-
)+λ
∵图象关于直线x=π对称,∴2πω-
=
+kπ,k∈z
∴ω=
+
,又ω∈(
,1)
∴k=1时,ω=
∴函数f(x)的最小正周期为
=
(2)∵f(
)=0
∴2sin(2×
×
-
)+λ=0
∴λ=-
∴f(x)=2sin(
x-
)-
由x∈[0,
]
∴
x-
∈[-
,
]
∴sin(
x-
)∈[-
,1]
∴2sin(
x-
)-
=f(x)∈[-1-
,2-
]
故函数f(x)在区间[0,
]上的取值范围为[-1-
,2-
]
| a |
| b |
| 3 |
=-(cos2ωx-sin2ωx)+
| 3 |
=
| 3 |
| π |
| 6 |
∵图象关于直线x=π对称,∴2πω-
| π |
| 6 |
| π |
| 2 |
∴ω=
| k |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴k=1时,ω=
| 5 |
| 6 |
∴函数f(x)的最小正周期为
| 2π | ||
2×
|
| 6π |
| 5 |
(2)∵f(
| π |
| 4 |
∴2sin(2×
| 5 |
| 6 |
| π |
| 4 |
| π |
| 6 |
∴λ=-
| 2 |
∴f(x)=2sin(
| 5 |
| 3 |
| π |
| 6 |
| 2 |
由x∈[0,
| 3π |
| 5 |
∴
| 5 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(
| 5 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
∴2sin(
| 5 |
| 3 |
| π |
| 6 |
| 2 |
| 2 |
| 2 |
故函数f(x)在区间[0,
| 3π |
| 5 |
| 2 |
| 2 |
点评:本题主要考查了y=Asin(ωx+φ)+k型函数的图象和性质,向量数量积运算性质,复合函数值域的求法,整体代入的思想方法,属基础题

练习册系列答案
相关题目
 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( )
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为( ) (2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )
(2012•湖北)已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )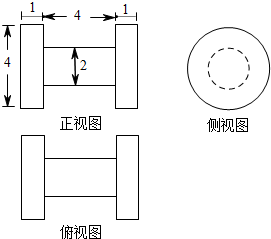 (2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为
(2012•湖北)已知某几何体的三视图如图所示,则该几何体的体积为