题目内容
函数 在一个周期内的图象如下,此函数的解析式为可为( ).
在一个周期内的图象如下,此函数的解析式为可为( ).
A. | B. |
C. | D. |
A
解析试题分析:根据题意,由图形可知函数的振幅为2,则可知A=2,同时周期为 ,然后代入点
,然后代入点
故可知解析式为 ,选A.
,选A.
考点:三角函数的解析式
点评:本试题考查的知识点是关于三角函数的解析式的求解,属于基础题。

练习册系列答案
相关题目
已知a是实数,则函数f(x)=1+asinax的图象不可能是( )
A. | B. |
C. | D. |
函数y=2sin(-2x+ )的单调减区间为( )
)的单调减区间为( )
A. | B. |
C. | D. |
已知点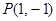 落在角
落在角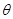 的终边上,则
的终边上,则 的值为( )
的值为( )
A.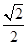 | B.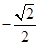 | C.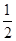 | D.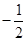 |
设函数
 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )
A. 在 在 单调递减 单调递减 | B. 在 在 单调递减 单调递减 |
C. 在 在 单调递增 单调递增 | D. 在 在 单调递增 单调递增 |
函数 的相邻两条对称轴之间的距离为 ( )
的相邻两条对称轴之间的距离为 ( )
A. | B. | C. | D. |
已知函数 的图象的一段圆弧(如图所示)
的图象的一段圆弧(如图所示) ,则( )
,则( )
A. | B. |
C. | D.前三个判断都不正确 |
已知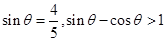 ,则
,则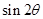 = ( )
= ( )
A.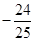 | B.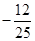 | C.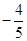 | D.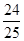 |
化简 等于
等于
A. | B. | C. | D. |