题目内容
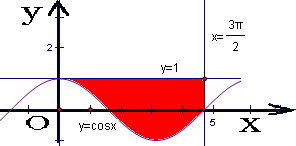
由函数y=cosx (0≤x≤
)的图象与直线x=
及y=1所围成的一个封闭图形的面积是( )
| 3π |
| 2 |
| 3π |
| 2 |
分析:根据题意结合定积分的几何意义,得所求面积为函数y=1-cosx在区间[0,
]上的积分,由此结合积分的计算公式和运算法则,不难求出本题的面积.
| 3π |
| 2 |
解答:解:由题意,所求面积为函数y=1-cosx在区间[0,
]上的积分,
∴S=
(1-cosx)dx=
,(其中C是任意常数)
=(
-sin
+C)-(0-sin0+C)=
+1
故选B
| 3π |
| 2 |

∴S=
| ∫ |
0 |
| (x-sinx+C)| |
0 |
=(
| 3π |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
故选B
点评:本题根据函数的图象,求一个封闭图形的面积,着重考查了积分的计算公式和运算法则,定积分的几何意义等知识点,属于基础题.

练习册系列答案
相关题目
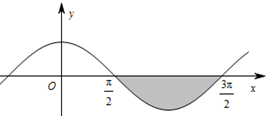
如图,阴影区域是由函数y=cosx的一段图象与x轴围成的封闭图形,那么这个阴影区域的面积是( )

| A、1 | ||
| B、2 | ||
C、
| ||
| D、π |
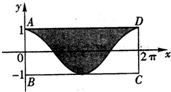 如图所示,墙上挂有一长为2π,宽为2的矩形木板ABCD,它的阴影部分是由函数y=cosx,x∈[0,2π]的图象和直线y=1围成的图形.某人向此板投镖,假设每次都能投中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是
如图所示,墙上挂有一长为2π,宽为2的矩形木板ABCD,它的阴影部分是由函数y=cosx,x∈[0,2π]的图象和直线y=1围成的图形.某人向此板投镖,假设每次都能投中木板,且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是 (2012•绵阳三模)已知函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<
(2012•绵阳三模)已知函数f(x)=Asin(wx+φ)(A>0,w>0,|φ|<