题目内容
设函数f（x）是R上的偶函数，且在区间（-∞，0）上增函数，有f（a2+2a+2）＜f（a2-2a+3）．求a的取值范围．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：根据函数奇偶性和单调性之间的关系，将不等式进行转化即可．
解答：
解：∵函数f（x）是R上的偶函数，且在区间（-∞，0）上增函数，
∴函数f（x）在区间（0，+∞）上减函数，
∵a2+2a+2=（a+1）2+1，a2-2a+3=（a-1）2+2，
∴不等式f（a2+2a+2）＜f（a2-2a+3）等价为a2+2a+2＞a2-2a+3．
即4a＞1，解得a＞
．
∴函数f（x）在区间（0，+∞）上减函数，
∵a2+2a+2=（a+1）2+1，a2-2a+3=（a-1）2+2，
∴不等式f（a2+2a+2）＜f（a2-2a+3）等价为a2+2a+2＞a2-2a+3．
即4a＞1，解得a＞
| 1 |
| 4 |
点评：本题考查函数奇偶性、单调性的应用，解决本题的关键是利用函数的单调性去掉不等式中的符号“f”，化为具体不等式．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
若0＜α＜
，0＜β＜
，且tanα=
，tanβ=
，则α+β等于（ ）
| π |
| 2 |
| π |
| 2 |
| 1 |
| 7 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
平面内，“动点P到两个定点的距离之和为正常数”是“动点P的轨迹是椭圆”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数f（x）=
-x3的图象关于（ ）
| 4 |
| x |
| A、坐标原点对称 |
| B、y轴对称 |
| C、直线y=-x对称 |
| D、直线y=x对称 |
在△ABC中，内角A、B、C的对边分别a、b、c，若
=
，sinC=2
sinB，则tana=（ ）
| a |
| b |
b+
| ||
| a |
| 3 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、-
|
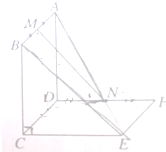如图，已知两个正方形ABCD和DCEF不在同一平面内，M，N分别为AB，DF的中点．