题目内容
已知
，则函数y=2f2（x）-3f（x）+1的零点的个数为________个．
4
分析：题中关于x的函数y=2f2（x）-3f（x）+1的零点问题，即要求方程2f2（x）-3f（x）+1=0的解的个数，对应于函数f（x）=1或f（x）=
的解的个数．故先根据题意作出f（x）的简图，由图可知，函数f（x）=1或f（x）=的解的个数，可以得出答案．
解答：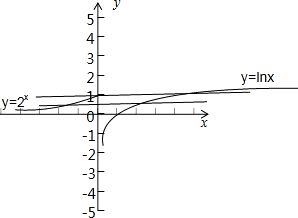
解：根据题意，令2f2（x）-3f（x）+1=0
得f（x）=1或f（x）=．
作出的简图：
由图象可得当f（x）=1或f（x）=
时，分别有3个和4个交点，
若关于x的函数y=2f2（x）-3f（x）+1的零点的个数为4．
故答案为：4．
点评：本题考查了函数的图象与一元二次方程根的分布的知识，采用数形结合的方法解决，使本题变得易于理解．数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
分析：题中关于x的函数y=2f2（x）-3f（x）+1的零点问题，即要求方程2f2（x）-3f（x）+1=0的解的个数，对应于函数f（x）=1或f（x）=
的解的个数．故先根据题意作出f（x）的简图，由图可知，函数f（x）=1或f（x）=的解的个数，可以得出答案．解答：
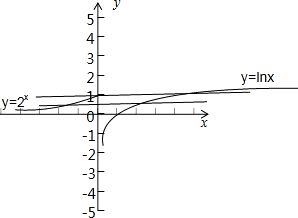解：根据题意，令2f2（x）-3f（x）+1=0得f（x）=1或f（x）=
．作出
的简图：由图象可得当f（x）=1或f（x）=
时，分别有3个和4个交点，
若关于x的函数y=2f2（x）-3f（x）+1的零点的个数为4．
故答案为：4．
点评：本题考查了函数的图象与一元二次方程根的分布的知识，采用数形结合的方法解决，使本题变得易于理解．数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
，则函数g（x）=f（2x）在（0，1）上有唯一零点；
的定义域中任意的x1、x2（x1≠x2）必有
；
，则函数g（x）=f（2x）在（0，1）上有唯一零点；
的定义域中任意的x1、x2（x1≠x2）必有
；