题目内容
（12分） 甲、乙两位篮球运动员进行定点投蓝，每人各投4个球，甲投篮命中的概率为
，乙投篮命中的概率为
．
(1)求甲至多命中2个且乙至少命中2个的概率；
(2)若规定每投篮一次命中得3分，未命中得
分，求乙所得分数
的概率分布和数学期望．
解：（1）设“甲至多命中2个球”为事件A，“乙至少命中两个球”为事件B，由题意得，
∴甲至多命中2个球且乙至少命中2个球的概率为
———————————————————4分
（2）
，分布列如下： 5分
P（=-4）=
P（=0）=
P（=4）=
P（=8）=
P（=12）=
8分
10分
12分
解析
练习册系列答案
相关题目
（本小题满分12分）
甲乙两名射手互不影响地进行射击训练，根据以往的数据统计，他们设计成绩的分布列如下：
| 射手甲 | 射手乙 | ||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 |
| 概率 |  | | | 概率 | |  |  |
（Ⅱ）若两个射手各射击1次，记所得的环数之和为
，求的分布列和期望． 
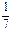．现有甲、乙两人从袋中轮流摸取1个球，甲先取，乙后取，然后甲再取，
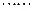，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的．求：
;9∶00~10∶00到站的客车B可能在9∶10，9∶30,
9∶50到站，其概率依次为
.
，求
；
,求
.
空气质量进行检测，空气质量分为A、B、C三级．
，
，执行如图所示的程序框图,如果输入
，则输出的
的值为
| A．7 | B．9 | C．2 | D．13 |
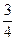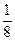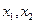，记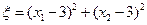
．
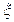取得最大值和最小值时的概率； （2）
求将3张不同的奥运会门票分给10名同学中的3人，每人1张，则不同的分法种数有( )
| A．2610 | B．720 | C．240 | D．120 |