题目内容
已知函数![]()
(1)求函数![]() 是单调区间;
是单调区间;
(2)如果关于![]() 的方程
的方程![]() 有实数根,求实数
有实数根,求实数![]() 的取值集合;
的取值集合;
(3)是否存在正数![]() ,使得关于x的方程
,使得关于x的方程![]() 有两个不相等的实数根?如果存在,求
有两个不相等的实数根?如果存在,求![]() 满足的条件;如果不存在,说明理由.
满足的条件;如果不存在,说明理由.
解:(1)函数![]() 的定义域是
的定义域是![]() 对
对![]() 求导得
求导得
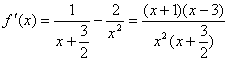 …………(2分)
…………(2分)
由 ![]() ,由
,由![]()
因此 ![]() 是函数
是函数![]() 的增区间;
的增区间;
(-1,0)和(0,3)是函数![]() 的减区间 ………………(5分)
的减区间 ………………(5分)
(2)因为![]()
所以实数m的取值范围就是函数![]() 的值域
的值域
对![]()
令![]()
∴当x=2时![]() 取得最大值,且
取得最大值,且![]()
又当x无限趋近于0时,![]() 无限趋近于
无限趋近于![]() 无限趋近于0,
无限趋近于0,
进而有![]() 无限趋近于-∞.因此
无限趋近于-∞.因此![]() 的值域是
的值域是 ![]()
即实数m的取值范围是![]() ………………(10分)
………………(10分)
(3)结论:这样的正数k不存在。 ………………(11分)
若存在正数k,使得关于x的方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() ,则
,则
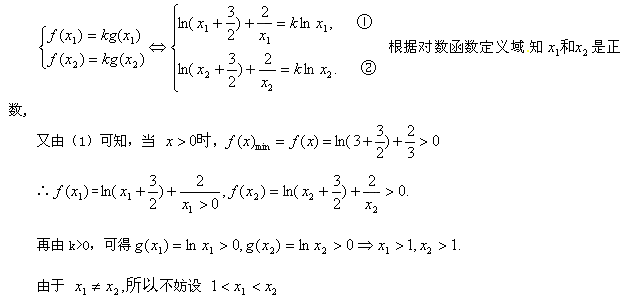
 由①和②可得
由①和②可得 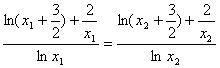
利用比例性质得 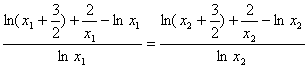
即 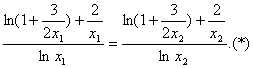 …………(13分)
…………(13分)
由于![]() 上的恒正增函数,且
上的恒正增函数,且 ![]()
又由于 ![]() 上的恒正减函数,且
上的恒正减函数,且 ![]()
∴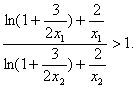
∴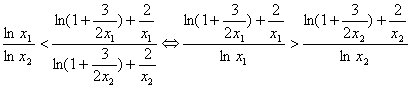
这与(*)式矛盾。因此满足条件的正数k不存在 ……………………15分

练习册系列答案
相关题目

 的单调递增区间;
的单调递增区间; 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 ,已知
,已知 ,
, 成等差数列,且
成等差数列,且 ,求边
,求边 的值.
的值.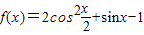
 ,且
,且 ,求sinx的值.
,求sinx的值.
 ,b=1,
,b=1, ,且a>b,试求角B和角C.
,且a>b,试求角B和角C.
 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小值;
上的最大值和最小值; ,求
,求 的值.
的值.