��Ŀ����
18����ƽ��ֱ������ϵxOy�У���OΪԭ�㣬��x�������Ὠ��������ϵ������C�ļ����귽��Ϊ��2-4��sin��+3=0��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=3+\frac{\sqrt{2}}{2}t}\end{array}\right.$����tΪ����������1��д������C��ֱ��l��ֱ�����귽�̣�
��2������A��B������C�ϵ������㣬��P��ֱ��l��һ���㣬���APB�����ֵ��
���� ��1������2=x2+y2����sin��=y���뼫���귽�̵ó�����C��ֱ�����귽�̣���ֱ��l�IJ���������ʽ�����ȥ����t���õ�ֱ��l����ͨ���̣�
��2������Բ��C��ֱ��l�ľ����ֱ֪����ԲC���룬��P��ԲC�����ߣ���OP��С��A��BΪ�е�ʱ����APB���
��� �⣺��1���ߦ�2-4��sin��+3=0��������C��ֱ�����귽��Ϊ��x2+y2-4y+3=0����x2+��y-2��2=1��
��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=1-\frac{\sqrt{2}}{2}t}\\{y=3+\frac{\sqrt{2}}{2}t}\end{array}\right.$����x-1+y-3=0����x+y-4=0��
��2������C��Բ��C��0��2����ֱ��l�ľ���d=$\frac{|2-4|}{\sqrt{2}}=\sqrt{2}$��1��
��ֱ��l��ԲC���룮
����P��ԲC�����ߣ���A��BΪ�е�ʱ����APB���
����OP��OA�����OPA=$\frac{1}{2}$��APB��sin��OPA=$\frac{OA}{OP}$=$\frac{1}{OP}$��
�൱OPȡ����Сֵ$\sqrt{2}$ʱ��sin��OPAȡ�����ֵ$\frac{\sqrt{2}}{2}$������OPA�����ֵΪ$\frac{��}{4}$��
���APB�����ֵΪ2��OPA=$\frac{��}{2}$��
���� ���⿼���˼����귽�̣�����������ֱ�����귽�̵Ļ���ת����ֱ����Բ��λ�ù�ϵ�������е��⣮

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�| A�� | 2 | B�� | 3 | C�� | 9 | D�� | 32 |
| ����������̨�� | 100 | 150 | 200 |
| Ƶ�� | 10 | 25 | 15 |
| Ƶ�� | 0.2 | 0.5 | 0.3 |
| ����������̨�� | 100 | 150 | 200 |
| Ƶ�� | 15 | 15 | 20 |
| Ƶ�� | 0.3 | 0.3 | 0.4 |
�����ϱ���Ƶ����Ϊ���ʣ���ÿ����������������
��1��������ƽ̨����һ��ƽ̨�ò�Ʒ�����������ȶ�Щ��
��2����A��Ϊ�о�������֪ÿ̨�õ�������������Ϊ0.2��ǧԪ�����æα�ʾ���ֵ���2����������ĺͣ���λ��ǧԪ������εķֲ��к���ѧ������
| A�� | [-$\sqrt{3}$��+�ޣ� | B�� | ��-�ޣ�$\sqrt{3}$] | C�� | [-$\sqrt{3}$��3�� | D�� | [-$\sqrt{3}$��+$\sqrt{3}$] |
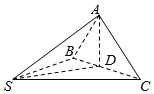 ��ͼ��ʾ����������S-ABC�У�SA=SB=SC=1����ASB=��ASC=60�㣬��BSC=90�㣬D��BC���е㣮��֤��
��ͼ��ʾ����������S-ABC�У�SA=SB=SC=1����ASB=��ASC=60�㣬��BSC=90�㣬D��BC���е㣮��֤��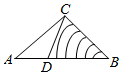 ��ͼ��B��C����֮�䲻��ֱ�ӵ��Ϊ����B��C�����ľ��루��λ��ǧ�ף�����ȷ��һ��ֱ��AD��ʹ��A��D��B���㹲�ߣ��ҡ�ADCΪ�۽ǣ��ֲ�á�BCD=60�㣬��A=45�㣬CD=$\sqrt{6}$-$\sqrt{2}$��AC=$\sqrt{2}$����CDB=�ȣ�
��ͼ��B��C����֮�䲻��ֱ�ӵ��Ϊ����B��C�����ľ��루��λ��ǧ�ף�����ȷ��һ��ֱ��AD��ʹ��A��D��B���㹲�ߣ��ҡ�ADCΪ�۽ǣ��ֲ�á�BCD=60�㣬��A=45�㣬CD=$\sqrt{6}$-$\sqrt{2}$��AC=$\sqrt{2}$����CDB=�ȣ�