题目内容
4名学生被人大、清华、北大录取，若每所大学至少要录取1名，则共有不同的录取方法（ ）
| A．72种 | B．36种 | C．24种 | D．12种 |
B
解析试题分析：将4名学生首先分成3组，共有
种方法，将3组分配到3个学校共有
种方法，所以不同的录取方法共有
种
考点：排列组合
点评：求解此类题目一般依据分步计数原理将其分为分组分配两步完成，分组时利用组合，分配时利用排列
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某餐厅有
四个桌子，每个桌子最多坐8人，现有11人进入餐厅，随意的坐下吃饭，已知
桌一定有人坐，其他桌子可能有人坐，也可能没人坐，则四个桌子坐的人数的不同的情况有多少种（ ）
| A．286 | B．276 | C．264 | D．246 |
二项式
的展开式的第二项的系数为
，则
的值为（ ）
A． | B． | C．或 | D．或 |
将5列车停在5条不同的轨道上，其中列车甲不停在第一轨道上，列车乙不停在第二轨道上，则不同的停放方法有 （ ）
| A．70种 | B．72种 | C．76种 | D．78种 |
(1+2x) 6的展开式中，x的系数等于
，则函数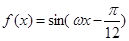
的最小正周期是
A． | B． | C． | D． |
的展开式中，只有第5项的二项式系数最大，则展开式中的第6项是 （） 
已知
的最小值为
，则二项式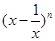
展开式中
项的系数为（ ）
A． | B． | C． | D． |
展开式的第6项系数最大，则其常数项为（ ）
| A．120 | B．252 | C．210 | D．45 |
将4本不同的书全发给3名同学，则每名同学至少有一本书的概率为（ ）
A． | B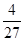． | C． | D． |