题目内容
过双曲线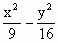 =1的右焦点F作倾角为
=1的右焦点F作倾角为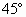 的直线l交双曲线于A、B两点,求AB中点C到F的距离.
的直线l交双曲线于A、B两点,求AB中点C到F的距离.
答案:
解析:
提示:
解析:
|
解:双曲线的焦点为F(5,0),∵l的倾角为 故 ∴|CF|= 分析 设法用A、B两点的坐标表示点C的坐标,再用两点间的距离公式求|CF|. |
提示:
|
本题考查双曲线的焦点,直线的点斜式方程及两点间距离公式等基本概念,这里利用韦达定理及中点公式,避免了求A、B、C的坐标的繁琐计算,这种技巧在求解有关圆锥曲线弦的问题时经常用到,应予以足够的重视. |

练习册系列答案
相关题目
 ,∴k=1,故l的方程为y=x-5代入双曲线方程,化简整理得:
,∴k=1,故l的方程为y=x-5代入双曲线方程,化简整理得: +90x-369=0①,设A(
+90x-369=0①,设A( ),B(
),B( ),C(
),C( ),则
),则 为①的两根.
为①的两根.
 .
.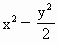 =1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有
=1的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有 =1的右焦点F作不垂直于x轴的直线交双曲线于M,N两点,MN的中垂线交x轴于R,求证:
=1的右焦点F作不垂直于x轴的直线交双曲线于M,N两点,MN的中垂线交x轴于R,求证: 为定值.
为定值.