题目内容
(08年西城区抽样测试理)(14分)
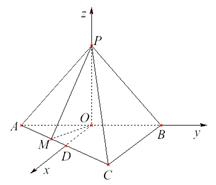
如图,在三棱锥![]() 中,
中,![]() ,
,![]()
![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求异面直线![]() 和
和![]() 所成角的大小.
所成角的大小.
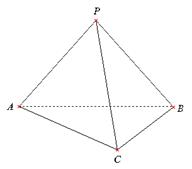
解析:解法一:
(Ⅰ)证明:
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() ,
, ![]() . ………….. 2分
. ………….. 2分
![]() 平面
平面 ![]() ,
, ![]() .
.
又![]()
![]()
![]() . ………….. 4分
. ………….. 4分
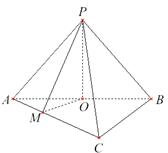
(Ⅱ)作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连结
,连结![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
, ![]() ,
,
根据三垂线定理得 ![]() ,
,
![]() 是二面角
是二面角![]() 的平面角. ………….. 6分
的平面角. ………….. 6分
设![]() ,
, ![]()
![]() .
.
![]() ,
, ![]() ,
,
![]() , ………….. 8分
, ………….. 8分
即二面角![]() 的大小是
的大小是![]() . ………….. 9分
. ………….. 9分
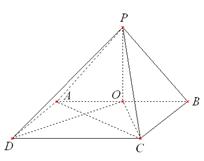
(Ⅲ)在底面![]() 内分别过
内分别过![]() 作
作![]() 的平行线,交于点
的平行线,交于点![]() ,
,
连结![]() .
.
则![]() 是异面直线
是异面直线![]() 和
和![]() 所成的角或其补角. ….. 11分
所成的角或其补角. ….. 11分
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
易知底面![]() 为矩形,从而
为矩形,从而![]() ,
,![]()
在![]() 中,
中,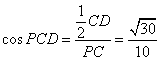 , ………….. 13分
, ………….. 13分
![]() 异面直线
异面直线![]() 和
和![]() 所成角的大小为
所成角的大小为![]() . ………….. 14分
. ………….. 14分
解法二:
作![]() 于点
于点![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 于点
于点![]() .
.
如图,以![]() 为原点,直线
为原点,直线![]() 分别为
分别为![]() 轴,
轴,
![]() 轴,
轴,![]() 轴,建立空间直角坐标系 .
轴,建立空间直角坐标系 .
![]() .
. ![]()
![]() .
.
![]() ,
,
![]() .
.
![]()
![]()
![]() ………….. 4分
………….. 4分
(Ⅰ)证明:
![]()
![]()
![]() .
.
又![]()
![]()
![]() . ………….. 7分
. ………….. 7分
(Ⅱ)作![]() 于点
于点![]() ,连结
,连结![]() .
.
![]() 平面
平面![]() , 根据三垂线定理得
, 根据三垂线定理得 ![]() ,
,
![]() 是二面角
是二面角![]() 的平面角. ………….. 8分
的平面角. ………….. 8分
在![]() 中,
中, ![]() ,
,
![]() 从而
从而![]() ,
,
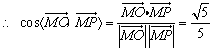 , ………….. 10分
, ………….. 10分
即二面角![]() 的大小是
的大小是![]() . ………….. 11分
. ………….. 11分
(Ⅲ)![]() ,
,
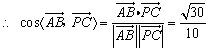 ,
,
![]() 异面直线
异面直线![]() 和
和![]() 所成角的大小为
所成角的大小为![]() . ………….. 14分
. ………….. 14分

 通城学典默写能手系列答案
通城学典默写能手系列答案