题目内容
(13分)已知圆C的方程为x2+(y﹣4)2=4,点O是坐标原点.直线l:y=kx与圆C交于M,N两点.
(Ⅰ)求k的取值范围;
(Ⅱ)设Q(m,n)是线段MN上的点,且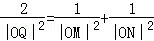 .请将n表示为m的函数.
.请将n表示为m的函数.
(Ⅰ)求k的取值范围;
(Ⅱ)设Q(m,n)是线段MN上的点,且
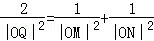 .请将n表示为m的函数.
.请将n表示为m的函数.(Ⅰ)(﹣∞,﹣ )∪(
)∪( ,+∞)(Ⅱ)n=
,+∞)(Ⅱ)n=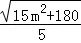 (m∈(﹣
(m∈(﹣ ,0)∪(0,
,0)∪(0, ))
))
 )∪(
)∪( ,+∞)(Ⅱ)n=
,+∞)(Ⅱ)n=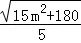 (m∈(﹣
(m∈(﹣ ,0)∪(0,
,0)∪(0, ))
))(Ⅰ)将y=kx代入x2+(y﹣4)2=4中,得:(1+k2)x2﹣8kx+12=0(*),
根据题意得:△=(﹣8k)2﹣4(1+k2)×12>0,即k2>3,
则k的取值范围为(﹣∞,﹣ )∪(
)∪( ,+∞);
,+∞);
(Ⅱ)由M、N、Q在直线l上,可设M、N坐标分别为(x1,kx1),(x2,kx2),
∴|OM|2=(1+k2)x12,|ON|2=(1+k2)x22,|OQ|2=m2+n2=(1+k2)m2,
代入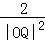 =
=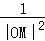 +
+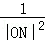 得:
得: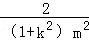 =
=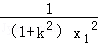 +
+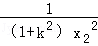 ,
,
即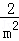 =
=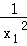 +
+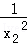 =
=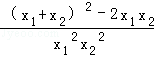 ,
,
由(*)得到x1+x2=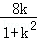 ,x1x2=
,x1x2=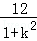 ,
,
代入得: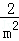 =
=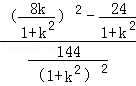 ,即m2=
,即m2=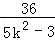 ,
,
∵点Q在直线y=kx上,∴n=km,即k= ,代入m2=
,代入m2=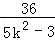 ,化简得5n2﹣3m2=36,
,化简得5n2﹣3m2=36,
由m2=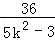 及k2>3,得到0<m2<3,即m∈(﹣
及k2>3,得到0<m2<3,即m∈(﹣ ,0)∪(0,
,0)∪(0, ),
),
根据题意得点Q在圆内,即n>0,
∴n=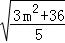 =
=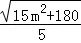 ,
,
则n与m的函数关系式为n=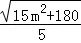 (m∈(﹣
(m∈(﹣ ,0)∪(0,
,0)∪(0, )).
)).
根据题意得:△=(﹣8k)2﹣4(1+k2)×12>0,即k2>3,
则k的取值范围为(﹣∞,﹣
 )∪(
)∪( ,+∞);
,+∞);(Ⅱ)由M、N、Q在直线l上,可设M、N坐标分别为(x1,kx1),(x2,kx2),
∴|OM|2=(1+k2)x12,|ON|2=(1+k2)x22,|OQ|2=m2+n2=(1+k2)m2,
代入
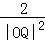 =
=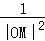 +
+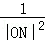 得:
得: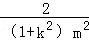 =
=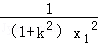 +
+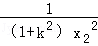 ,
,即
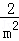 =
=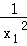 +
+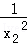 =
=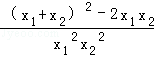 ,
,由(*)得到x1+x2=
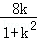 ,x1x2=
,x1x2=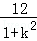 ,
,代入得:
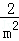 =
=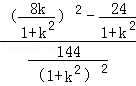 ,即m2=
,即m2=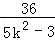 ,
,∵点Q在直线y=kx上,∴n=km,即k=
 ,代入m2=
,代入m2=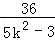 ,化简得5n2﹣3m2=36,
,化简得5n2﹣3m2=36,由m2=
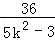 及k2>3,得到0<m2<3,即m∈(﹣
及k2>3,得到0<m2<3,即m∈(﹣ ,0)∪(0,
,0)∪(0, ),
),根据题意得点Q在圆内,即n>0,
∴n=
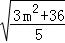 =
=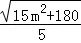 ,
,则n与m的函数关系式为n=
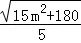 (m∈(﹣
(m∈(﹣ ,0)∪(0,
,0)∪(0, )).
)).
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
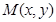 到定点
到定点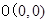 与到定点
与到定点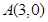 的距离之比为
的距离之比为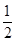 .
.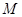 的轨迹C的方程,并指明曲线C的轨迹;
的轨迹C的方程,并指明曲线C的轨迹;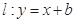 ,若曲线C上恰有三个点到直线
,若曲线C上恰有三个点到直线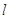 的距离为1,求实数
的距离为1,求实数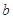 的值。
的值。 与曲线
与曲线 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( ) ,
, ]
] ,3]
,3] 经过点
经过点 ,当
,当 所得弦长最长时,直线
所得弦长最长时,直线



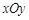 中,设点
中,设点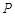 为圆
为圆 :
: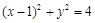 上的任意一点,点
上的任意一点,点 (2
(2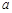 ,
,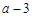 ) (
) (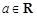 ),则线段
),则线段 长度的最小值为 .
长度的最小值为 . 被圆
被圆 截得的弦长为_______________.
截得的弦长为_______________. 上一动点,PA,PB是圆C:
上一动点,PA,PB是圆C: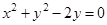 的两条切线,A、B是切点,若四边形PACB的最小面积是2,则
的两条切线,A、B是切点,若四边形PACB的最小面积是2,则 的值为
的值为  C.
C. D.2
D.2 截圆
截圆 所得的弦长是 .
所得的弦长是 . 的圆心为
的圆心为 ,直线
,直线 与圆
与圆 两点,且
两点,且 ,则圆
,则圆