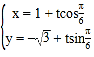题目内容
【题目】设函数![]() (
(![]() R).
R).
(1)求函数![]() 在R上的最小值;
在R上的最小值;
(2)若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有四个不相等的实数根,求
上有四个不相等的实数根,求![]() 的取值范围.
的取值范围.
【答案】(1) (2)
(2)![]() (3)
(3)![]()
【解析】
(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值;
(2)恒成立需要保证![]() 即可,对二次函数进行分析,根据取到最大值时的情况得到
即可,对二次函数进行分析,根据取到最大值时的情况得到![]() 的范围;
的范围;
(3)通过条件将问题转化为二次函数在给定区间上有两个零点求![]() 的范围,这里将所有满足条件的不等式列出来,求解出
的范围,这里将所有满足条件的不等式列出来,求解出![]() 的范围.
的范围.
解:(1)令![]() ,
,![]() ,则
,则![]() ,对称轴为
,对称轴为![]() .
.
①![]() ,即
,即![]() ,
,![]() .
.
②![]() ,即
,即![]() ,
,![]() .
.
③![]() ,即
,即![]() ,
,![]() .
.
综上可知,
(2)由题意可知,![]() ,
,![]() ,
,![]() 的图象是开口向上的抛物线,最大值一定在端点处取得,所以有
的图象是开口向上的抛物线,最大值一定在端点处取得,所以有
![]() 故
故![]() .
.
(3)令![]() ,
,![]() .由题意可知,当
.由题意可知,当![]() 时,
时,![]() 有两个不等实数解,所以原题可转化为
有两个不等实数解,所以原题可转化为![]() 在
在![]() 内有两个不等实数根.所以有
内有两个不等实数根.所以有


练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目