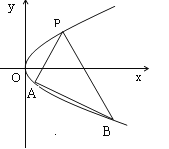
题目内容

【题目】已知抛物线的焦点为，准线为，在抛物线上任取一点，过做的垂线，垂足为.

（1）若，求的值；

（2）除外，的平分线与抛物线是否有其他的公共点，并说明理由.

【答案】(1)；(2)答案见解析.

【解析】

试题分析：（1）根据抛物线定义求A点坐标，得E点坐标，再根据向量数量积求的值；（2）设，根据得的平分线所在直线就是边上的高所在的直线.根据点斜式得的平分线所在的直线方程，再与抛物线联立，解方程组可得只有一解.

试题解析：（1），∴，即由抛物线的对称性，不防取

∵，∴，，

∴

（2）设，∵，，.

由知的平分线所在直线就是边上的高所在的直线.

∴的平分线所在的直线方程为.

由，消得.

∵，方程化为，即

即的平分线与只有一个公共点，除以外没有其他公共点.

练习册系列答案
相关题目

【题目】设函数（R）．

（1）求函数在R上的最小值；

（2）若不等式在上恒成立，求的取值范围；

（3）若方程在上有四个不相等的实数根，求的取值范围．

【题目】

在中，角A、B、C的对边分别为a、b、c，面积为S，已知

（Ⅰ）求证：成等差数列；

（Ⅱ）若求.

【题目】已知函数，．

（1）若在区间上不单调，求的取值范围；

（2）设，若函数在区间恒有意义，求实数的取值范围；

（3）已知方程在有两个不相等的实数根，求实数的取值范围．

【题目】已知函数（，且）.

（Ⅰ）求函数的单调区间；

（Ⅱ）求函数在上的最大值.

【答案】（Ⅰ）的单调增区间为，单调减区间为.（Ⅱ）当时， ；当时， .

【解析】【试题分析】(I)利用的二阶导数来研究求得函数的单调区间.(II) 由（Ⅰ）得在上单调递减，在上单调递增，由此可知.利用导数和对分类讨论求得函数在不同取值时的最大值.

【试题解析】

（Ⅰ），

设 ，则.

∵， ，∴在上单调递增，

从而得在上单调递增，又∵，

∴当时， ，当时， ，

因此， 的单调增区间为，单调减区间为.

（Ⅱ）由（Ⅰ）得在上单调递减，在上单调递增，

由此可知.

∵， ，

∴.

设，

则 .

∵当时， ，∴在上单调递增.

又∵，∴当时， ；当时， .

①当时， ，即，这时， ；

②当时， ，即，这时， .

综上， 在上的最大值为：当时， ；

当时， .

[点睛]本小题主要考查函数的单调性,考查利用导数求最大值. 与函数零点有关的参数范围问题，往往利用导数研究函数的单调区间和极值点，并结合特殊点，从而判断函数的大致图像，讨论其图象与轴的位置关系，进而确定参数的取值范围；或通过对方程等价变形转化为两个函数图象的交点问题．

【题型】解答题
【结束】
22

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，圆的普通方程为. 在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为 .

（Ⅰ） 写出圆 的参数方程和直线的直角坐标方程；

（ Ⅱ ） 设直线 与轴和轴的交点分别为，为圆上的任意一点，求的取值范围.

【题目】已知两个定点，， 动点满足，设动点的轨迹为曲线，直线：.

（1）求曲线的轨迹方程；

（2）若与曲线交于不同的、两点，且 (为坐标原点)，求直线的斜率；

（3）若，是直线上的动点，过作曲线的两条切线、，切点为、，探究：直线是否过定点，若存在定点请写出坐标，若不存在则说明理由.

【题目】如图，在四棱锥中，是正三角形，四边形是正方形.

（Ⅰ）求证：；

（Ⅱ）若，求直线与平面所成角的正弦值.

【题目】如图，抛物线关于轴对称，它的顶点在坐标原点，点、、均在抛物线上.

（1）写出该抛物线的方程及其准线方程；

（2）当与的斜率存在且倾斜角互补时，求的值及直线的斜率.

【题目】某几何体的三视图如图所示，则该几何体的体积为（ ）

A. 64 B. 32 C. 96 D. 48

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网