题目内容
已知椭圆E:
+
=1(a>b>0)长轴长是短轴长的
倍,且经过点A(
,
),直线x=t与椭圆E交于不同的两点M,N,以线段MN为直径作圆C,圆心为C.
(1)求椭圆E的方程;
(2)若圆C与y轴相交,求实数t的取值范围;
(3)设Q(x,y)是圆C上的动点,当t变化时,求x的最大值.
| x2 |
| b2 |
| y2 |
| a2 |
| 3 |
| ||
| 3 |
| 2 |
(1)求椭圆E的方程;
(2)若圆C与y轴相交,求实数t的取值范围;
(3)设Q(x,y)是圆C上的动点,当t变化时,求x的最大值.
分析:(1)根据椭圆长轴和短轴之间的关系,结合椭圆过定点A(
,
),得到关于a,b的二元方程组,求解a,b后即可得到答案;
(2)把直线x=t与椭圆方程联立,求出圆的半径,利用圆心C到y轴的距离小于半径求解t的取值范围;
(3)直接由圆的方程解出x,利用放缩法去掉y,再运用三角函数换元,最后由三角函数的值域求最值.
| ||
| 3 |
| 2 |
(2)把直线x=t与椭圆方程联立,求出圆的半径,利用圆心C到y轴的距离小于半径求解t的取值范围;
(3)直接由圆的方程解出x,利用放缩法去掉y,再运用三角函数换元,最后由三角函数的值域求最值.
解答:解:(1)依题意得:a:b=
,且椭圆经过点A(
,
),
∴
⇒a2=3,b2=1.
则椭圆E的方程为x2+
=1;
(2)由题意知圆心C(t,0)(-1<t<1).
由
⇒y2=3(1-t2),
∴圆C的半径为r=
.
∵圆C与y轴相交,且圆心C到y轴的距离d=|t|,
∴|t|<
?t2<3(1-t2)?-
<t<
,
即实数t的取值范围(-
,
);
(3)圆C的方程为(x-t)2+y2=3(1-t2).
∵点Q(x,y)在圆C上,∴x=t±
.
∵t-
≤t+
,
故只需求x=t+
的最大值.
x=t+
≤t+
(y=0时,等号成立).
设t=cosθ,θ∈(0,π),则t+
=cosθ+
sinθ=2sin(θ+
),
当θ=
,即t=
,且y=0时,x取最大值2.
| 3 |
| ||
| 3 |
| 2 |
∴
|
则椭圆E的方程为x2+
| y2 |
| 3 |
(2)由题意知圆心C(t,0)(-1<t<1).
由
|
∴圆C的半径为r=
| 3(1-t2) |
∵圆C与y轴相交,且圆心C到y轴的距离d=|t|,
∴|t|<
| 3(1-t2) |
| ||
| 2 |
| ||
| 2 |
即实数t的取值范围(-
| ||
| 2 |
| ||
| 2 |
(3)圆C的方程为(x-t)2+y2=3(1-t2).
∵点Q(x,y)在圆C上,∴x=t±
| 3(1-t2)-y2 |
∵t-
| 3(1-t2)-y2 |
| 3(1-t2)-y2 |
故只需求x=t+
| 3(1-t2)-y2 |
x=t+
| 3(1-t2)-y2 |
| 3(1-t2) |
设t=cosθ,θ∈(0,π),则t+
| 3(1-t2) |
| 3 |
| π |
| 6 |
当θ=
| π |
| 3 |
| 1 |
| 2 |
点评:本题考查了椭圆的标准方程、椭圆的简单几何性质,考查了直线和圆锥曲线的关系,解答(3)时运用换元法,体现了放缩思想方法,思维难度较大.该题属高考试题中的压轴题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
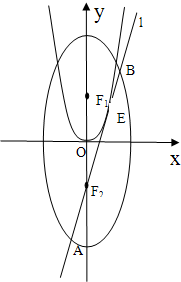 如图,已知椭圆
如图,已知椭圆