题目内容
17. 已知某三棱锥的三视图如图所示,则它的外接球体积为$\frac{4}{3}π$.
已知某三棱锥的三视图如图所示,则它的外接球体积为$\frac{4}{3}π$.
分析 画出几何体的图形,判断三棱锥的形状,求出外接球的半径即可.
解答  解:由题意考查几何体的图形如图,
解:由题意考查几何体的图形如图,
该几何体是一个底面为直角三角形,顶点在底面的射影为斜边中点的三棱锥,
三棱锥的数据如图,
此几何体的外接球半径为1,体积为$\frac{4}{3}π$.
故答案为:$\frac{4}{3}π$.
点评 本题考查球的半径的求法,考查空间想象能力以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$则目标函数z=3x+y的最大值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 14 |
5.在四棱锥V-ABCD中,B1,D1分别为侧棱VB、VD的中点,则四面体AB1CD1的体积与四棱锥V-ABCD的体积之比为( )
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
2.已知集合={x|1-x>0},B={x|2x>1},则A∩B=( )
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x>1} |
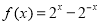 ,数列
,数列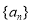 满足
满足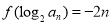 .
.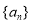 的通项公式;
的通项公式;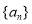 是递减数列.
是递减数列. 中,
中, ,
, ,求此数列的通项公式.
,求此数列的通项公式.