Question

如图，在四棱锥S-ABCD中，AB⊥AD，AB∥CD，CD=3AB，平面SAD⊥平面ABCD，M是线段AD上一点，AM=AB，DM=DC，SM⊥AD．
（1）证明：BM⊥平面SMC；
（2）设三棱锥C-SBM与四棱锥S-ABCD的体积分别为V₁与V，求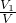的值．

Answer 1

解：（1）证明：∵平面SAD⊥平面ABCD，平面SAD∩平面ABCD=AD，SM?平面SAD，SM⊥AD
∴SM⊥平面ABCD，（1分）
∵BM?平面ABCD，∴SM⊥BM．（2分）
∵四边形ABCD是直角梯形，AB∥CD，AM=AB，DM=DC，
∴△MAB，△MDC都是等腰直角三角形，
∴∠AMB=∠CMD=45°，∠BMC=90°，BM⊥CM．（4分）
∵SM?平面SMC，CM?平面SMC，SM∩CM=M，
∴BM⊥平面SMC（6分）
（2）三棱锥C-SBM与三棱锥S-CBM的体积相等，
由（1）知SM⊥平面ABCD，
得，（9分）
设AB=a，由CD=3AB，AM=AB，DM=DC，
得，
从而．（12分）
分析：（1）证明BM⊥平面SMC，由题意及图形，先证SM⊥BM，再证BM⊥CM，然后由线面垂直的判定定理直接得出结论即可．
（2）由图形知，三棱锥C-SBM与三棱锥S-CBM的体积相等，而三棱锥S-CBM与四棱锥S-ABCD等高，故体积比可以转化成面积比，代入数据计算既得．
点评：本题综合考查了面面垂直的性质定理，线面垂直的判定定理，线面垂直的性质定理以及棱锥的体积公式等，涉及到的知识较多，综合性很强，对答题者根据题设条件及要解决的问题进行知识的重新组合、灵活转化的能力要求较高．