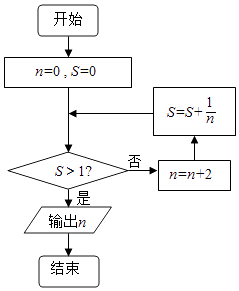
题目内容
【题目】在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2. (Ⅰ)求证:AC∥平面DEF;
(Ⅱ)若二面角D﹣AB﹣E为直二面角,
( i)求直线AC与平面CDE所成角的大小;
( ii)棱DE上是否存在点P,使得BP⊥平面DEF?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.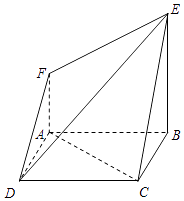
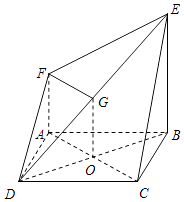
【答案】证明:(Ⅰ)连结BD,设AC∩BD=O, 因为四边形ABCD为正方形,所以O为BD中点.
设G为DE的中点,连结OG,FG,
则OG∥BE,且 ![]() .
.
由已知AF∥BE,且 ![]() ,所以AF∥OG,OG=AF.
,所以AF∥OG,OG=AF.
所以四边形AOGF为平行四边形.
所以AO∥FG,即AC∥FG.
因为AC平面DEF,FG平面DEF,
所以AC∥平面DEF.
解:(Ⅱ)(i)由已知,AF∥BE,AB⊥BE,所以AF⊥AB.
因为二面角D﹣AB﹣E为直二面角,所以平面ABCD⊥平面ABEF.
所以AF⊥平面ABCD,所以AF⊥AD,AF⊥AB.
四边形ABCD为正方形,所以AB⊥AD.所以AD,AB,AF两两垂直.
以A为原点,AD,AB,AF分别为x,y,z轴建立空间直角坐标系(如图).
因为AB=BE=2AF=2,
所以A(0,0,0),B(0,2,0),C(2,2,0),D(2,0,0),E(0,2,2),F(0,0,1),
所以 ![]() .
.
设平面CDE的一个法向量为n=(x,y,z),
由 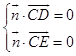 得
得 ![]() 即
即 ![]()
取x=1,得n=(1,0,1).
设直线AC与平面CDE所成角为θ,
则 ![]() ,
,
因为0≤θ≤90°,所以θ=30°.
即直线AC与平面CDE所成角的大小为30°.
(ii)假设棱DE上存在点P,使得BP⊥平面DEF.
设 ![]() ,则
,则 ![]() .
.
设P(x,y,z),则 ![]() ,
,
因为 ![]() ,所以(x﹣2,y,z)=λ(﹣2,2,2).
,所以(x﹣2,y,z)=λ(﹣2,2,2).
所以x﹣2=﹣2λ,y=2λ,z=2λ,所以P点坐标为(2﹣2λ,2λ,2λ).
因为B(0,2,0),所以 ![]() .
.
又 ![]() ,
,
所以 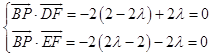 ,解得
,解得 ![]() .
.
因为 ![]() ,所以DE上存在点P,使得BP⊥平面DEF,且
,所以DE上存在点P,使得BP⊥平面DEF,且 ![]() .
.
(另解)假设棱DE上存在点P,使得BP⊥平面DEF.
设 ![]() ,则
,则 ![]() .
.
设P(x,y,z),则 ![]() ,
,
因为 ![]() ,所以(x﹣2,y,z)=λ(﹣2,2,2).
,所以(x﹣2,y,z)=λ(﹣2,2,2).
所以x﹣2=﹣2λ,y=2λ,z=2λ,所以P点坐标为(2﹣2λ,2λ,2λ).
因为B(0,2,0),所以 ![]() .
.
设平面DEF的一个法向量为 ![]() =(x0 , y0 , z0),
=(x0 , y0 , z0),
则  ,由
,由 ![]() ,得
,得 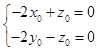
取x0=1,得 ![]() =(1,﹣1,2).
=(1,﹣1,2).
由 ![]() ,即(2﹣2λ,2λ﹣2,2λ)=μ(1,﹣1,2),
,即(2﹣2λ,2λ﹣2,2λ)=μ(1,﹣1,2),
可得 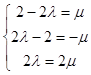 解得
解得 ![]() .
.
因为 ![]() ,所以DE上存在点P,使得BP⊥平面DEF,且
,所以DE上存在点P,使得BP⊥平面DEF,且 ![]() .…(14分)
.…(14分)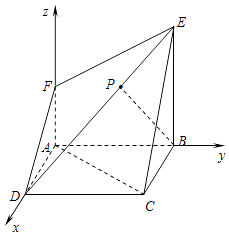
【解析】(Ⅰ)连结BD,设AC∩BD=O,设G为DE的中点,连结OG,FG,推导出四边形AOGF为平行四边形,从而AC∥FG,由此能证明AC∥平面DEF. (Ⅱ)(i)以A为原点,AD,AB,AF分别为x,y,z轴建立空间直角坐标系,利用向量法能求出直线AC与平面CDE所成角的大小.(ii)假设棱DE上存在点P,使得BP⊥平面DEF.设 ![]() ,则
,则 ![]() .设P(x,y,z),求出P点坐标为(2﹣2λ,2λ,2λ),从而
.设P(x,y,z),求出P点坐标为(2﹣2λ,2λ,2λ),从而 ![]() .由此能求出DE上存在点P,使得BP⊥平面DEF,且
.由此能求出DE上存在点P,使得BP⊥平面DEF,且 ![]() . (另解)假设棱DE上存在点P,使得BP⊥平面DEF.设
. (另解)假设棱DE上存在点P,使得BP⊥平面DEF.设 ![]() ,则
,则 ![]() .设P(x,y,z),求出平面DEF的一个法向量,由此能求出DE上存在点P,使得BP⊥平面DEF,且
.设P(x,y,z),求出平面DEF的一个法向量,由此能求出DE上存在点P,使得BP⊥平面DEF,且 ![]() .
.
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则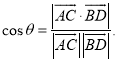 .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案