题目内容
(本小题10分)选修4—1:几何证明选讲
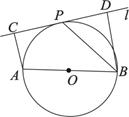
如图,设![]() 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,![]() 是⊙O与l的公共点,
是⊙O与l的公共点,
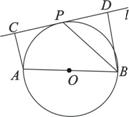
![]() ⊥l,
⊥l,![]() ⊥l,垂足分别为
⊥l,垂足分别为![]() ,
,![]() ,且
,且![]() ,求证:
,求证:
(I)l是⊙O的切线;
(II)![]() 平分∠ABD.
平分∠ABD.
|
选修4—1:几何证明选讲
证明:(Ⅰ)连结OP,因为AC⊥l,BD⊥l,
所以AC//BD.
又OA=OB,PC=PD,
所以OP//BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线. ……………………5分
(Ⅱ)连结AP,因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.……………………10分
|

练习册系列答案
相关题目
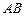 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,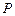 是⊙O与l的公共点,
是⊙O与l的公共点,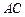 ⊥l,
⊥l,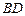 ⊥l,垂足分别为
⊥l,垂足分别为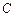 ,
,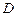 ,且
,且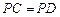 ,
,
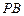 平分∠ABD.
平分∠ABD. (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。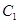 的参数方程为
的参数方程为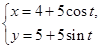 (
(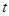 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,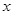 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线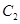 的极坐标方程为
的极坐标方程为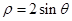 。
。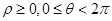 )。
)。 版权所有:(www.k s 5 u.com)
版权所有:(www.k s 5 u.com)