题目内容
(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
【答案】
(1)因为 ,消去参数,得
,消去参数,得 ,即
,即 ,
,
故 极坐标方程为
极坐标方程为 ;
;
(2) 的普通方程为
的普通方程为 ,联立
,联立 、
、 的方程,解得
的方程,解得 或
或 ,所以交点的极坐标为
,所以交点的极坐标为 .
.
【解析】(1)先得到C1的一般方程,进而得到极坐标方程;(2)先联立求出交点坐标,进而求出极坐标.
【考点定位】本题考查极坐标方程的应用以及转化,考查学生的转化与化归能力.

练习册系列答案
相关题目
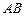 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径,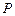 是⊙O与l的公共点,
是⊙O与l的公共点,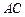 ⊥l,
⊥l,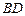 ⊥l,垂足分别为
⊥l,垂足分别为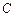 ,
,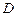 ,且
,且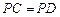 ,
,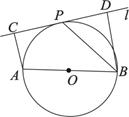
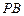 平分∠ABD.
平分∠ABD.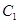 的参数方程为
的参数方程为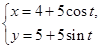 (
(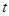 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,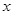 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线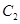 的极坐标方程为
的极坐标方程为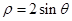 。
。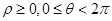 )。
)。 版权所有:(www.k s 5 u.com)
版权所有:(www.k s 5 u.com)