题目内容
下列说法正确的是 .
(1)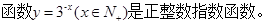 .
.
(2).函数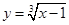 的定义域为
的定义域为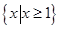
(3).函数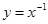 在
在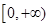 上是单调递减的
上是单调递减的
(4).函数是一种特殊的映射
(1)
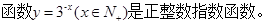 .
.(2).函数
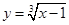 的定义域为
的定义域为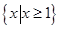
(3).函数
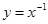 在
在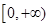 上是单调递减的
上是单调递减的(4).函数是一种特殊的映射
(1)(4)
因为 ,符合指数函数的定义,成立。
,符合指数函数的定义,成立。
函数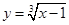 的定义域为
的定义域为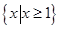 错误,应该是全体实数,函数
错误,应该是全体实数,函数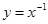 在
在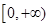 上是单调递减的,不成立,.函数是一种特殊的映射成立。故填写(1)(4)
上是单调递减的,不成立,.函数是一种特殊的映射成立。故填写(1)(4)
 ,符合指数函数的定义,成立。
,符合指数函数的定义,成立。函数
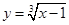 的定义域为
的定义域为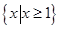 错误,应该是全体实数,函数
错误,应该是全体实数,函数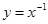 在
在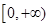 上是单调递减的,不成立,.函数是一种特殊的映射成立。故填写(1)(4)
上是单调递减的,不成立,.函数是一种特殊的映射成立。故填写(1)(4)
练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 ,
, 的值; (10分)
的值; (10分)
 恒成立,求m的取值范围
恒成立,求m的取值范围 在区间
在区间 上单调递增,则实数a的取值范围是__________。
上单调递增,则实数a的取值范围是__________。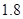 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若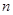 天购买一次,需要支付
天购买一次,需要支付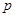 是多少元?[
是多少元?[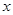 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这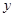 (元)关于
(元)关于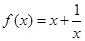 .
.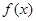 在
在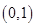 上是减函数;
上是减函数;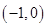 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).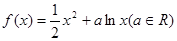 .
.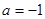 ,求
,求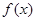 的单调递增区间;
的单调递增区间;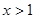 时,
时,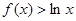 恒成立,求实数
恒成立,求实数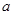 的取值范围.
的取值范围. 图像的是( )
图像的是( )