题目内容
已知函数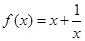 .
.
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明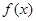 在
在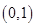 上是减函数;
上是减函数;
(3)函数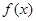 在
在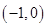 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
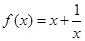 .
.(1)判断函数的奇偶性,并加以证明;
(2)用定义证明
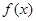 在
在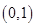 上是减函数;
上是减函数;(3)函数
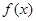 在
在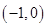 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).证明:(I)函数为奇函数
(II)设 且
且


.
 .
.

因此函数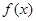 在
在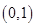 上是减函数
上是减函数
(III)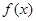 在
在 上是减函数.
上是减函数.

(II)设
 且
且


.

 .
.
因此函数
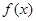 在
在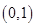 上是减函数
上是减函数(III)
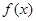 在
在 上是减函数.
上是减函数.本题考查函数的性质,考查学生的计算能力,证明函数的单调性按照取值、作差、变形定号,下结论的步骤进行.
(1)函数为奇函数.确定函数的定义域,利用奇函数的定义,即可得到结论;
(2)按照取值、作差、变形定号,下结论的步骤进行证明,作差后要因式分解
(1)函数为奇函数.确定函数的定义域,利用奇函数的定义,即可得到结论;
(2)按照取值、作差、变形定号,下结论的步骤进行证明,作差后要因式分解

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 ,当
,当 时,
时, ,那么
,那么 时,
时, .
.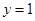 ,
,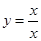
 ,
,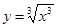
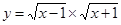 ,
,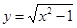
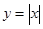 ,
,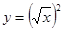
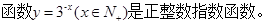 .
.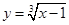 的定义域为
的定义域为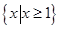
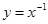 在
在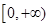 上是单调递减的
上是单调递减的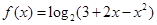 .
. 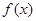 的定义域;
的定义域;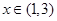 上是减函数;
上是减函数; 上单调递增的函数是( )
上单调递增的函数是( )



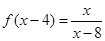 ,则函数
,则函数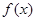 = ( )
= ( )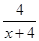
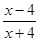
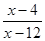
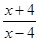

 ,若
,若 ,则x=
,则x=  ,则
,则 ( )
( )