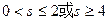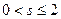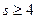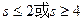题目内容
某单位决定投资 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价 元,两侧墙砌砖,每米造价
元,两侧墙砌砖,每米造价 元,顶部每平方米造价
元,顶部每平方米造价 元,试问:(1)仓库面积
元,试问:(1)仓库面积 的最大允许值是多少?(2)为使
的最大允许值是多少?(2)为使 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
 元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价
元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米造价 元,两侧墙砌砖,每米造价
元,两侧墙砌砖,每米造价 元,顶部每平方米造价
元,顶部每平方米造价 元,试问:(1)仓库面积
元,试问:(1)仓库面积 的最大允许值是多少?(2)为使
的最大允许值是多少?(2)为使 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?(1) 的最大允许值是
的最大允许值是 平方米,(2)铁栅的长应是
平方米,(2)铁栅的长应是 米.
米.

 的最大允许值是
的最大允许值是 平方米,(2)铁栅的长应是
平方米,(2)铁栅的长应是 米.
米.
如图,设铁栅长为 米,一堵砖墙长为
米,一堵砖墙长为 米,则有
米,则有 ,
,
由题意得 ,
,
应用二元均值不等式,
得


∴ ,即
,即 ,
,
∵ ,∴
,∴ ,∴
,∴ .
.
因此, 的最大允许值是
的最大允许值是 平方米,取得此最大值的条件是
平方米,取得此最大值的条件是 ,
,
而 ,求得
,求得 ,即铁栅的长应是
,即铁栅的长应是 米.
米.
 米,一堵砖墙长为
米,一堵砖墙长为 米,则有
米,则有 ,
,由题意得
 ,
,应用二元均值不等式,
得



∴
 ,即
,即 ,
,∵
 ,∴
,∴ ,∴
,∴ .
.因此,
 的最大允许值是
的最大允许值是 平方米,取得此最大值的条件是
平方米,取得此最大值的条件是 ,
,而
 ,求得
,求得 ,即铁栅的长应是
,即铁栅的长应是 米.
米.
练习册系列答案
相关题目
 表示的平面区域.
表示的平面区域.

 则满足条件
则满足条件 的点
的点 所形成区域的面积为( )
所形成区域的面积为( )


 满足
满足 ,若不等式
,若不等式 恒成立,求
恒成立,求 最大值
最大值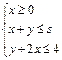 下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )
下,当3≤s≤5时,目标函数z=3x+2y的最大值的变化范围是( )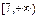
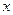 的实系数方程
的实系数方程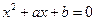 有两个根,一个根在区间
有两个根,一个根在区间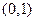 内,另一根在区间
内,另一根在区间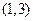 内,记点
内,记点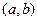 对应的区域为
对应的区域为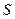 .
.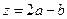 ,求
,求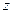 的取值范围;
的取值范围;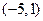 的一束光线,射到
的一束光线,射到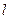 经过区域
经过区域 满足条件
满足条件 ,则
,则 的轨迹形成的图形的面积为1,则
的轨迹形成的图形的面积为1,则 .
.  的最大值为 .
的最大值为 . 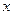 、
、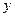 满足条件
满足条件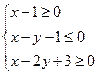 ,则
,则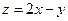 的最小值为 .
的最小值为 .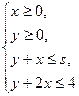 表示的平面区域是一个三角形,则实数s的取值范围是( )
表示的平面区域是一个三角形,则实数s的取值范围是( )