题目内容
已知等差数列{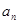 }的首项a1=1,公差d>0,且
}的首项a1=1,公差d>0,且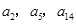 分别是等比数列{
分别是等比数列{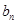 }的b2,b3,b4.
}的b2,b3,b4.
(I)求数列{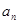 }与{{
}与{{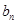 }的通项公式;
}的通项公式;
(Ⅱ)设数列{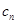 }对任意自然数n均有
}对任意自然数n均有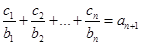 成立,求
成立,求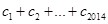 的值.
的值.
【答案】
(I)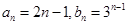 ;(II)
;(II)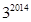 .
.
【解析】
试题分析:(I)首先建立公差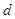 的方程,确定得到等差数列的通项公式;再根据
的方程,确定得到等差数列的通项公式;再根据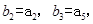 求得
求得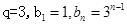 .
.
(II)根据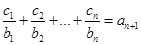 ①
①
建立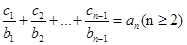 ②
②
两式相减得到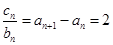
通过验证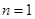 ,不适合上式,确定得到
,不适合上式,确定得到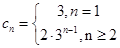 ,从而求得
,从而求得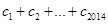 .
.
试题解析:(I)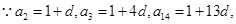 且
且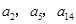 等比数列,
等比数列,
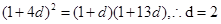 ,
,
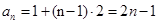 ,
,
又因为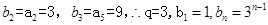
(II)因为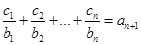 ①
①
所以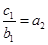 即
即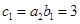 ,
,
又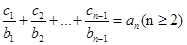 ②
②
①-②: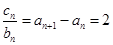
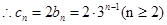 ,
,
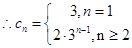
则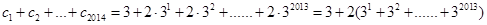
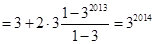
考点:等差数列、等比数列,数列的通项,数列的求和.

练习册系列答案
相关题目
 (2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2005•静安区一模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数