题目内容
已知函数 ,其中a,b∈R
,其中a,b∈R
(1)当a=3,b=-1时,求函数f(x)的最小值;
(2)若曲线y=f(x)在点(e,f(e))处的切线方程为2x-3y-e=0(e=2.71828 为自然对数的底数),求a,b的值;
(3)当a>0,且a为常数时,若函数h(x)=x[f(x)+lnx]对任意的x1>x2≥4,总有 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.
 ,其中a,b∈R
,其中a,b∈R(1)当a=3,b=-1时,求函数f(x)的最小值;
(2)若曲线y=f(x)在点(e,f(e))处的切线方程为2x-3y-e=0(e=2.71828 为自然对数的底数),求a,b的值;
(3)当a>0,且a为常数时,若函数h(x)=x[f(x)+lnx]对任意的x1>x2≥4,总有
 成立,试用a表示出b的取值范围.
成立,试用a表示出b的取值范围.(1)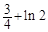 ;(2)
;(2)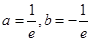 ;(3)
;(3)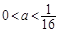 时,
时,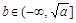 ,
,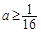 时,
时,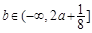
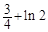 ;(2)
;(2)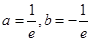 ;(3)
;(3)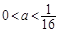 时,
时,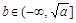 ,
,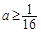 时,
时,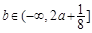
试题分析:(1)利用导数判断出函数
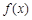 的单调性,即可求出
的单调性,即可求出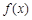 的最小值;(2)要注意给出某点处的切线方程,就既有该点的坐标,也有该点出切线的斜率,利用这两个条件可求出a与b的值;(3)解决本题的关键是由“对任意的x1>x2≥4,总有
的最小值;(2)要注意给出某点处的切线方程,就既有该点的坐标,也有该点出切线的斜率,利用这两个条件可求出a与b的值;(3)解决本题的关键是由“对任意的x1>x2≥4,总有 成立”转化出“
成立”转化出“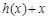 在
在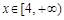 上单调递增”,从而再次转化为导函数大于0的问题求解.解题过程中要注意对参数的合理分类讨论.
上单调递增”,从而再次转化为导函数大于0的问题求解.解题过程中要注意对参数的合理分类讨论.试题解析:(1)当a=3,b=-1时,
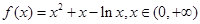
∴
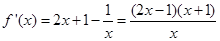
∵x>0,∴0<x<
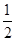 时f '(x)<0,x>
时f '(x)<0,x>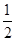 时,f '(x)>0
时,f '(x)>0即
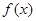 在
在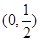 上单调递减,在
上单调递减,在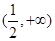 上单调递增
上单调递增∴
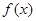 在
在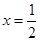 处取得最小值
处取得最小值即
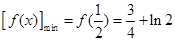 4分
4分(2)∵
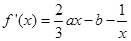
∴
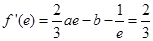 (1)
(1)又切点(e,f(e))在直线2x-3y-e=0上
∴切点为
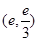
∴
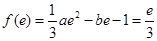 (2)
(2)联立(1)(2),解得
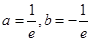 . 8分
. 8分(3)由题意,对任意的x1>x2≥4,总有
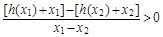 成立
成立令
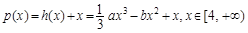
则函数p(x)在
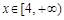 上单调递增
上单调递增∴
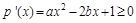 在
在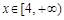 上恒成立
上恒成立∴
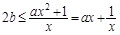 在
在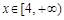 上恒成立 10分
上恒成立 10分构造函数
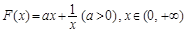
则
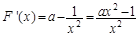
∴F(x)在
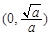 上单调递减,在
上单调递减,在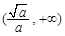 上单调递增
上单调递增(i)当
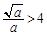 ,即
,即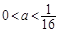 时,F(x)在
时,F(x)在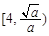 上单调递减,在
上单调递减,在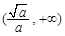 上单调递增
上单调递增∴
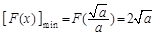
∴
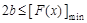 ,从而
,从而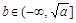 12分
12分(ii)当
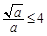 ,即
,即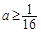 时,F(x)在(4,+∞)上单调递增
时,F(x)在(4,+∞)上单调递增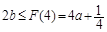 ,从而
,从而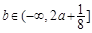 13分
13分综上,当
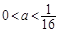 时,
时,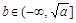 ,
,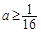 时,
时,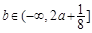 14分
14分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 的函数
的函数 ,其导函数为
,其导函数为 .记函数
.记函数 在区间
在区间 上的最大值为
上的最大值为 .
. 在
在 处有极值
处有极值 ,试确定
,试确定 的值;
的值; ,证明对任意的
,证明对任意的 ,都有
,都有 ;
; 对任意的
对任意的 的最大值.
的最大值. x2+ax+b,g(x)=x3+
x2+ax+b,g(x)=x3+ x2+ 1nx+b,(a,b为常数).
x2+ 1nx+b,(a,b为常数). ,直线
,直线 与函数
与函数 的图象都相切于点
的图象都相切于点 .
.  的解析式;
的解析式; (其中
(其中 是
是 的导函数),求函数
的导函数),求函数 的值域.
的值域.
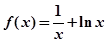 的极小值为 ;
的极小值为 ; ,函数
,函数 的导函数
的导函数 是奇函数,若曲线
是奇函数,若曲线 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
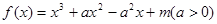
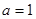 时,函数
时,函数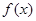 有三个互不相同的零点,求
有三个互不相同的零点,求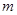 的取值范围;
的取值范围;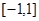 内没有极值点,求
内没有极值点,求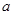 的取值范围;
的取值范围;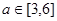 ,不等式
,不等式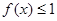 在
在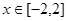 上恒成立,求实数
上恒成立,求实数 在点
在点 处的切线的方程是 。
处的切线的方程是 。