题目内容
△ABC中,A,C为锐角,角A,B,C所对的边之长依次为a,b,c,且sinA=
,cos2C=
.
(1)求cos(A+C)的值;
(2)若a-c=
-1,求a,b,c的值.
| ||
| 5 |
| 4 |
| 5 |
(1)求cos(A+C)的值;
(2)若a-c=
| 2 |
分析:(1)△ABC中,由cos2C=
及二倍角余弦公式求得sinC、cosC的值,再由sinA的值求得cosA的值,再利用两角和差的余弦公式求得cos(A+C)的值.
(2)应用正弦定理,由条件求得2R的值,再利用正弦定理的变形a=2RsinA、b=2RsinB、c=2RsinC求出结果.
| 4 |
| 5 |
(2)应用正弦定理,由条件求得2R的值,再利用正弦定理的变形a=2RsinA、b=2RsinB、c=2RsinC求出结果.
解答:解:(1)△ABC中,由 cos2C=
及二倍角余弦公式、A,B是锐角求得sinC=
,cosC=
.(3分)
再由sinA=
,得cosA=
,(4分)
∴cos(A+C)=cosAcosC-sinAsinC=
×
-
×
=
.(6分)
(2)应用正弦定理,由条件得2RsinA-2RsinC=
-1,得2R=
,( 9分)
故 sinB=sin(A+C)=
,
∴a=2RsinA=
;b=2RsinB=
;c=2RsinC=1.(12分)
| 4 |
| 5 |
| 1 | ||
|
| 3 | ||
|
再由sinA=
| 1 | ||
|
| 2 | ||
|
∴cos(A+C)=cosAcosC-sinAsinC=
| 2 | ||
|
| 3 | ||
|
| 1 | ||
|
| 1 | ||
|
| ||
| 2 |
(2)应用正弦定理,由条件得2RsinA-2RsinC=
| 2 |
| 10 |
故 sinB=sin(A+C)=
| ||
| 2 |
∴a=2RsinA=
| 2 |
| 5 |
点评:本题主要考查正弦定理和余弦定理的应用,两角和差的正弦、余弦公式、二倍角公式的应用,属于中档题.

练习册系列答案
相关题目
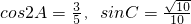 .
.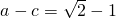 ,求a,b,c的值;
,求a,b,c的值;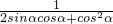 的值.
的值.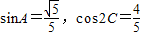 .
.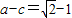 ,求a,b,c的值.
,求a,b,c的值.