题目内容
设
，
是两个非零向量，则（ ）
| a |
| b |
分析：通过向量特例，判断A的正误；利用向量的垂直判断矩形的对角线长度相等，判断B的正误；通过特例直接判断向量共线，判断正误；
通过反例直接判断结果不正确即可．
通过反例直接判断结果不正确即可．
解答：解：对于A，不妨设
=（3，0），
=（-1，0），显然|
+
|=|
|-|
|，但是
与
不垂直，而是共线，所以A不正确．
对于B，若
⊥
，则
•
=0，故有|
+
|=|
-
|，所以，|
+
|=|
|-|
| 不正确．
对于C，若|
+
|=|
|-|
|，则存在实数λ，使得
=λ
，例如，
=（3，0），
=（-1，0），显然
=-
，所以C正确．
对于D，不妨设
=（3，0），
=（1，0），显然
=
，但是|
+
|=|
|-|
|不正确．
综上，只有C正确，
故选C．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
对于B，若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
对于C，若|
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
| 1 |
| 3 |
| a |
对于D，不妨设
| a |
| b |
| b |
| 1 |
| 3 |
| a |
| a |
| b |
| a |
| b |
综上，只有C正确，
故选C．
点评：本题考查向量的关系的综合应用，特例法的具体应用，考查计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
，
是两个非零向量，则“向量
，
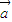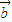是两个非零向量，则“向量
，
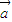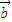的夹角为锐角”是“函数f（x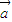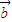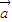）=（x
+
）•（
-x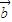
）的图象是一条开口向下的抛物线”的（ ）