题目内容
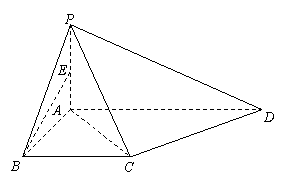
如图，在四棱锥
中，底面
为直角梯形，且
，
，侧面
底面，
. 若
.
（Ⅰ）求证：
平面
；
（Ⅱ）设侧棱
的中点是
，求证：
平面
.
 |
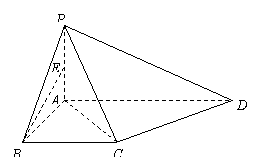
解：（Ⅰ）因为 ，
所以
.
又因为侧面底面，
且侧面
底面
，
所以
底面.
 |
而
底面，
所以
.
在底面中，
因为
，，
所以 
， 所以
.
又因为
， 所以平面. ……………………………6分
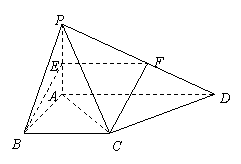
（Ⅱ）设侧棱
的中点为
，
连结
，
，
，
则
，且
.
由已知，
所以
. 又
，
所以
. 且
.
所以四边形
为平行四边形，所以
.
因为
平面，
平面，
所以平面. ………………………………………………………13分
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
中，底面
是矩形．已知
．
平面
；
与
所成的角的大小；
的大小．
中，底面
是菱形，
，
，
,
平面
是
的中点，
是
的中点. 
∥平面
；
；
所成的锐二面角的大小.
中，底面
是矩形．已知
．
平面
；
与
所成的角的大小；
的大小．
中，底面
是正方形，侧棱
，
为
中点，作
交
于
与平面
所成的锐二面角的正弦值。
中，底面
为平行四边形，
平面
在棱
上．
时，求证
平面
的大小为
时，求直线
与平面
所成角的正弦值．