题目内容
如图所示,一个半圆和长方形组成的铁皮,长方形的边 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形 ,使得
,使得 ,
, .
.
(1)设 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.
(1)三角形铁皮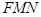 的面积为
的面积为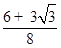 ;(2)
;(2) 的面积的最大值为
的面积的最大值为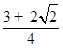 .
.
解析试题分析:(1)先根据题中条件得出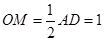 ,
,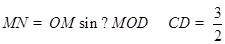 ,
,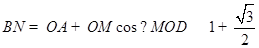 ,最后根据三角形的面积计算公式
,最后根据三角形的面积计算公式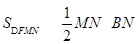 即可得到所求的三角形的面积;(2)先引入角度作为变量,即设
即可得到所求的三角形的面积;(2)先引入角度作为变量,即设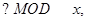 ,进而根据(1)中思路求出
,进而根据(1)中思路求出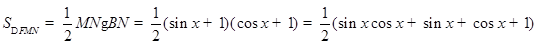 ,到此用同角三角函数的基本关系式,进行换元,令
,到此用同角三角函数的基本关系式,进行换元,令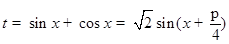 ,先确定
,先确定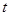 的取值范围,进而得到
的取值范围,进而得到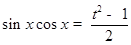 ,从而
,从而 ,根据求出的
,根据求出的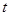 的取值范围,结合二次函数的图像与性质即可确定
的取值范围,结合二次函数的图像与性质即可确定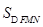 的最大值.
的最大值.
(1)由题意知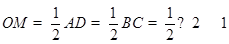
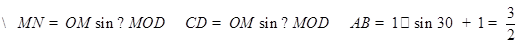
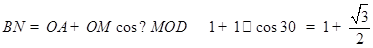
 ,即三角形铁皮
,即三角形铁皮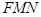 的面积为
的面积为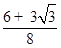
(2)设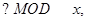 则
则 ,
,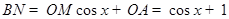 ,
,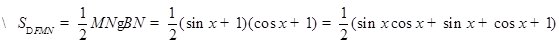
令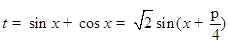 ,由于
,由于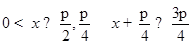 ,则有
,则有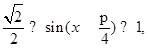 所以
所以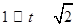
且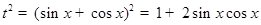 ,所以
,所以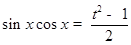
故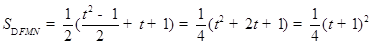
而函数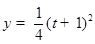 在区间
在区间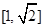 上单调递增
上单调递增
故当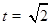 时,
时,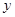 取得最大值
取得最大值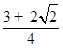 .
.
考点:1.三角函数的实际应用;2.同角三角函数的基本关系式;3.三角函数的图像与性质;4.二次函数的图像与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ).
). 的最小正周期;
的最小正周期;  ,求
,求 的值.
的值. 的部分图象如图所示.
的部分图象如图所示. 的最小正周期及图中
的最小正周期及图中 、
、 的值;
的值;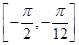 上的最大值和最小值.
上的最大值和最小值.
 )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
.
 时,求函数
时,求函数 的最小值和最大值;
的最小值和最大值; ABC的内角A,B,C的对应边分别为a,b,c,且c=
ABC的内角A,B,C的对应边分别为a,b,c,且c= ,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值.
,f(C)=2,若向量m=(1,a)与向量n=(2,b)共线,求a,b的值. 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为 .
. ,求点A的坐标.
,求点A的坐标. .
.