题目内容
已知函数
)．
(1)求函数
的最小正周期；
(2)若
，求
的值．
(1)π;(2)
．
解析试题分析：（1）先将函数化为
的形式，再由
求得周期;(2)由
得到sin
＝
．由
得到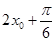
的范围，欲求，可进行拆角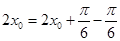
，利用和差化积公式解得．
试题解析： (1)由f(x)＝2
sin xcos x＋2cos2x－1，得f(x)＝ (2sin xcos x)＋(2cos2x－1)＝sin 2x＋cos 2x＝2sin
，所以函数f(x)的最小正周期为π．(2)由(1)可知f(x0)＝2sin．又因为f(x0)＝
，所以sin＝．由，得
,从而cos＝
．所以cos 2x0＝
＝coscos
＋sin
sin＝．（12分）
考点：1、三角函数的化简；2、拆角．
练习册系列答案
相关题目
的最小正周期和单调递减区间；
中，
分别是角A、B、C的对边，若
,求
，
.
的最小正周期；
上的值域.
，定义一种向量积
．
，
，点
为
的图象上的动点，点
为
的图象上的动点，且满足
（其中
为坐标原点）．
表示
； 
倍（纵坐标不变），得到函数
的图象.设函数
，试讨论函数
在区间
内的零点个数.
的最小正周期及单调递减区间；
个单位，得到函数
的图像，求
上的最大值和最小值，并求出相应的x的取值。
，并写出函数
的最小正周期；
为非零常数，且
，试问
是周期函数吗？证明你的结论.
．
的最小正周期和单调增区间；
，求
为半圆的直径，
为半圆的圆心，
，
，现要将此铁皮剪出一个三角形
，使得
，
.
，求三角形铁皮
，若
，则
．