题目内容
若函数 的图象与直线y=m相切,相邻切点之间的距离为
的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且 ,求点A的坐标.
,求点A的坐标.
(1)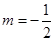 或
或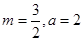 ;(2)
;(2)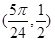 或
或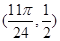 .
.
解析试题分析:(1)利用二倍角公式的降幂变形以及辅助角公式,可以把 变形为
变形为 ,又根据条件
,又根据条件 的图像与直线y=m相切,可知m为函数
的图像与直线y=m相切,可知m为函数 的最大值或最小值,即
的最大值或最小值,即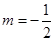 或
或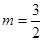 ,而相邻两个点之间的距离即相邻两条对称轴之间的距离即为函数的周期
,而相邻两个点之间的距离即相邻两条对称轴之间的距离即为函数的周期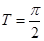 ,从而求得a=2;(2)根据正弦函数
,从而求得a=2;(2)根据正弦函数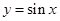 的对称中心为
的对称中心为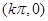 ,可令
,可令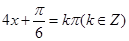 ,解得
,解得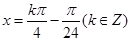 ,即
,即 ,又有
,又有 ,可求得整数k的值为1或2,从而可以得到对称中心的坐标为
,可求得整数k的值为1或2,从而可以得到对称中心的坐标为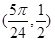 或
或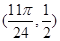 .
.
(1) ,
,
由题意 的图像与直线y=m相切,∴m为
的图像与直线y=m相切,∴m为 的最大值或最小值,即
的最大值或最小值,即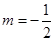 或
或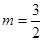 ;
;
又∵相邻两切点之间的距离为 ,∴函数
,∴函数 的周期为
的周期为 ,∴
,∴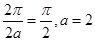 ;
;
(2)由(1)可知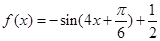 ,
,
令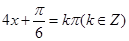 ,解得
,解得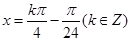 ,
,
即 ,又∵
,又∵ ,∴
,∴ ,解得
,解得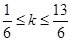 ,∵
,∵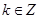 ,∴k=1或k=2,∴点A的坐标为
,∴k=1或k=2,∴点A的坐标为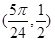 或
或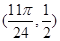 .
.
考点:1、三角恒等变形;2、三角函数的图像与性质.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 .
. 的最小正周期和单调增区间;
的最小正周期和单调增区间; ,求
,求 为半圆的直径,
为半圆的直径, 为半圆的圆心,
为半圆的圆心, ,
, ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形 ,使得
,使得 ,
, .
. ,求三角形铁皮
,求三角形铁皮

 时,求函数
时,求函数 取得最大值和最小值;
取得最大值和最小值; 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是 ,且
,且 ,若向量
,若向量 与向量
与向量 平行,求
平行,求 的值.
的值. 0,
0, .
. 值; (2)求
值; (2)求 的值.
的值. +
+ +
+ (
( 为常数)
为常数) 的最小正周期;
的最小正周期; 上的最大值与最小值之和为
上的最大值与最小值之和为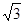 ,求实数
,求实数 的值.
的值.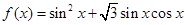 .
. 的值;
的值;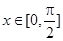 时,求函数
时,求函数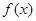 的最大值和最小值.
的最大值和最小值.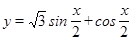 的图像,并说明这个图像是由
的图像,并说明这个图像是由 的图像经过怎样的变换得到的.
的图像经过怎样的变换得到的.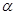 ,△EFC的面积为
,△EFC的面积为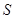 .
.