题目内容
工厂需要围建一个面积为512m2 的矩形堆料场,一过可以利用原有的墙壁,其他三边需要砌新的墙壁,我们知道,砌起的新墙的总长度y(单位:m)是利用原有墙壁长度x(单位:m)的函数.
(1)写出y关于x的函数解析式,确定x的取值范围:
(2)随着x的变化,y的变化有何规律?
(3)堆料场的长、宽比为多少时,需要砌起的新墙用的材料最省?
(1)写出y关于x的函数解析式,确定x的取值范围:
(2)随着x的变化,y的变化有何规律?
(3)堆料场的长、宽比为多少时,需要砌起的新墙用的材料最省?
考点:函数解析式的求解及常用方法,函数模型的选择与应用
专题:函数的性质及应用
分析:(1)由题意可得矩形与墙面垂直的边长为
,由面积可得x和y的方程,变形可得函数解析式,由实际意义可得x的范围;(2)求导数可得单调性,可得y的变化规律;(3)由(2)可得函数的极值点,可得最值点,可得所求.
| y-x |
| 2 |
解答:
解:(1)由题意可得矩形与墙面垂直的边长为
,
且
•x=512,变形可得y=x+
,
由题意可得x>0,
(2)由(1)知y=x+
,求导数可得y′=1-
,
令1-
<0可解得0<x<32,
故当x∈(0,32)时,函数y=x+
单调递减,
当x∈(32,+∞)时,函数y=x+
单调递增;
(3)由(2)知,函数y=x+
在x=32处取到极小值,
唯一的极小值也是最小值,此时y=64,
=16,
故长和宽分别为32和16时,用料最省.
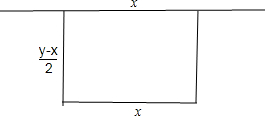
| y-x |
| 2 |
且
| y-x |
| 2 |
| 1024 |
| x |
由题意可得x>0,
(2)由(1)知y=x+
| 1024 |
| x |
| 1024 |
| x2 |
令1-
| 1024 |
| x2 |
故当x∈(0,32)时,函数y=x+
| 1024 |
| x |
当x∈(32,+∞)时,函数y=x+
| 1024 |
| x |
(3)由(2)知,函数y=x+
| 1024 |
| x |
唯一的极小值也是最小值,此时y=64,
| y-x |
| 2 |
故长和宽分别为32和16时,用料最省.
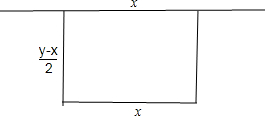
点评:本题考查函数解析式的求解,涉及导数法求函数的最值,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目