题目内容
函数f(x)=
ax3+
ax2-2ax+2a+1的图象经过四个象限,则实数a的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A.a>-
| B.-
| C.a>-
| D.-
|
f′(x)=ax2+ax-2a=a(x+2)(x-1)
令f′(x)=a(x+2)(x-1)=0得x=-2或x=1
x∈(-∞,-2)时f′(x)的符号与x∈(-2,1)时f′(x)的符号相反,x∈(-2,1)时f′(x)的符号与x∈(1,+∞)时f′(x)的符号相反
∴f(-2)=-
a+2a+4a+2a+1=
a+1和为极值,f(1)=
a+
a-2a+2a+1=
a+1
∵图象经过四个象限
∴f(-2)•f(1)<0即(
a+1)(
a+1)<0
解得-
<a<-
故答案为B
令f′(x)=a(x+2)(x-1)=0得x=-2或x=1
x∈(-∞,-2)时f′(x)的符号与x∈(-2,1)时f′(x)的符号相反,x∈(-2,1)时f′(x)的符号与x∈(1,+∞)时f′(x)的符号相反
∴f(-2)=-
| 8 |
| 3 |
| 16 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 6 |
∵图象经过四个象限
∴f(-2)•f(1)<0即(
| 16 |
| 3 |
| 5 |
| 6 |
解得-
| 6 |
| 5 |
| 3 |
| 16 |
故答案为B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
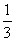 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).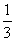 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).