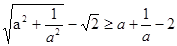题目内容
用分析法证明：若a＞0，则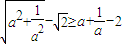
．
【答案】分析：根据a＞0，寻找使不等式
成立的充分条件，直到使不等式成立的充分条件已经显然
具备为止．
解答：证明：∵a＞0，要证
，只要证 
，
只要证
+4
+4≥
+2
（
）+4，
即证 2
≥
（
）．
只要证4（
）≥2（
+2），即证
≥2．
由基本不等式可得
≥2 成立，故原不等式成立．
点评：本题主要考查基本不等式的应用，用分析法证明不等式，利用用分析法证明不等式的关键是寻找使不等式成立的
充分条件，直到使不等式成立的充分条件已经显然具备为止，属于中档题．
成立的充分条件，直到使不等式成立的充分条件已经显然具备为止．
解答：证明：∵a＞0，要证
，只要证 ，只要证
+4+4≥+2（）+4，即证 2
≥（）．只要证4（
）≥2（+2），即证≥2．由基本不等式可得
≥2 成立，故原不等式成立．点评：本题主要考查基本不等式的应用，用分析法证明不等式，利用用分析法证明不等式的关键是寻找使不等式成立的
充分条件，直到使不等式成立的充分条件已经显然具备为止，属于中档题．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
