题目内容
(理)设数列{an}的前n项和为Sn,满足(4-p)Sn+3pan=2p+4,其中p为常数,且p<-2,n∈N*.(1)求证:数列{an}是等比数列,并求出数列{an}的通项公式;
(2)若数列{an}的公比q=f(p),数列{bn}满足b1=a1,bn=![]() f(bn-1)(n≥2),求数列{bn}的通项公式;
f(bn-1)(n≥2),求数列{bn}的通项公式;
(3)在(2)的条件下,若![]() (bnlgan)=lg(
(bnlgan)=lg(![]() p),求实数p的值.
p),求实数p的值.
(文)设数列{an}的前n项和为Sn,满足(4-p)Sn+3pan=2p+4,其中p为常数,且p<-2,n∈N*.
(1)求a1并证明数列{an}是等比数列;
(2)若p=-4,求a4的值;
(3)若数列{an}的公比q=f(p),数列{bn}满足b1=a1,bn=![]() f(bn-1)(n≥2),求数列{bn}的通项公式.
f(bn-1)(n≥2),求数列{bn}的通项公式.
答案:(理)(1)证明:当n=1时,由(4-p)a1+3pa1=2p+4,得(2p+4)a1=2p+4.∵p<-2,2p+4≠0,∴a1=1.
又由(4-p)Sn+3pan=2p+4,(4-p)Sn-1+3pan-1=2p+4(n≥2).
两式相减得(4-p)an+3p(an-an-1)=0,(4+2p)an=3pan-1.故![]() (n≥2).
(n≥2).
∴数列{an}是以1为首项、![]() 为公比的等比数列.
为公比的等比数列.
∴an=![]() .
.
(2)解:f(p)=![]() ,b1=a1=1.∵bn=
,b1=a1=1.∵bn=![]() f(bn-1)=
f(bn-1)=![]() (n≥2),
(n≥2),
∴![]() ,即
,即![]() (n≥2).
(n≥2).
故数列{![]() }是以
}是以![]() =1为首项、
=1为首项、![]() 为公差的等差数列.
为公差的等差数列.
∴![]() =1+
=1+![]() (n-1)=
(n-1)=![]() .∴bn=
.∴bn=![]() (n≥1).
(n≥1).
(3)解:由![]() (bnlgan)=lg(
(bnlgan)=lg(![]() ),
),
又bnlgan=![]() lg(
lg(![]() )n-1=
)n-1=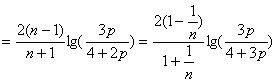 ,
,
∴![]() (bnlgan)=2lg(
(bnlgan)=2lg(![]() )=lg(
)=lg(![]() ).∴(
).∴(![]() )2=
)2=![]() .
.
化简为p2+5p+4=0,解得p=-1与p=-4.由题意知p<-2,故舍去-1,得p=-4.
(文)解:(1)当n=1时,由(4-p)a1+3pa1=2p+4,得(2p+4)a1=2p+4.
∵p<-2,2p+4≠0,∴a1=1.
又由(4-p)Sn+3pan=2p+4,(4-p)Sn-1+3pan-1=2p+4(n≥2),两式相减得(4-p)an+3p(an-an-1)=0.
(4+2p)an=3pan-1,故![]() =
=![]() (n≥2).
(n≥2).
∴数列{an}是以1为首项、![]() 为公比的等比数列.
为公比的等比数列.
(2)当p=-4时,公比q=![]() =3.
=3.
∴a4=a1q3=27.9分
(3)f(p)=![]() ,b1=a1=1,∵bn=
,b1=a1=1,∵bn=![]() f(bn-1)=
f(bn-1)=![]() ·
·![]() (n≥2),
(n≥2),
∴![]() ,即
,即![]() =
=![]() (n≥2).故数列{
(n≥2).故数列{![]() }是以
}是以![]() =1为首项、
=1为首项、![]() 为公差的等差数列.
为公差的等差数列.
∴![]() =1+
=1+![]() (n-1)=
(n-1)=![]() .∴bn=
.∴bn=![]() (n≥1).
(n≥1).

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案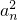 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设 求f(n)的最大值.
求f(n)的最大值. 成等差数列.(1)求通项an;(2)设
成等差数列.(1)求通项an;(2)设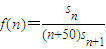 求f(n)的最大值.
求f(n)的最大值.