题目内容
6．已知集合A={1}，B={x|tx+2=0}，且A∪B=A，则t的取值范围为{0，-2}．分析 根据A∪B=A，便可得到B⊆A，从而考虑求出集合B中的x，这样需讨论t：t=0时，显然满足B⊆A；t≠0时，可以得到集合B={$-\frac{2}{t}$}，从而有$-\frac{2}{t}=1$，这样便可得出t的取值，也就得到了t的取值范围．
解答 解：A∪B=A；
∴B⊆A；
①若t=0，B=∅，满足B⊆A；
②若t≠0，则B={x|$x=-\frac{2}{t}$}；
B⊆A；
∴$-\frac{2}{t}=1$；
∴t=-2；
∴t的取值范围为：{0，-2}．
故答案为：{0，-2}．
点评 考查列举法、描述法表示集合，并集、子集的概念，并集的运算，不要漏了t=0的情况．
练习册系列答案
阅读快车系列答案
相关题目
16．使直线a，b为异面直线的充分不必要条件是（ ）
| A． | a?平面α，b?平面α，a与b不平行 | |
| B． | a?平面α，b?平面α，a与b不相交 | |
| C． | a∥直线c，b∩c=A，b与a不相交 | |
| D． | a?平面α，b?平面β，α∩β=l，a与b无公共点 |
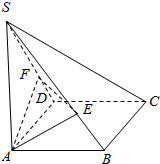如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD所在的平面，过点A分别作AE⊥SB，AF⊥SD，垂足分别为点E和点F，求证：EF⊥SC．